题目内容
 如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点F,AD与CE相交于点G,且CG=AB.
如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点F,AD与CE相交于点G,且CG=AB.(1)证明:∠B=∠CGD;
(2)证明:△ABD≌△CGD;
(3)求∠BCA的度数.
考点:全等三角形的判定与性质
专题:计算题
分析:(1)利用同角的余角相等得到一对角相等,再由对顶角相等,利用内角和定理即可得证;
(2)利用AAS即可得证;
(3)由三角形ABD与三角形CGD全等,利用全等三角形的对应边相等得到AD=DC,确定出三角形ADC为等腰直角三角形,即可求出∠BCA的度数.
(2)利用AAS即可得证;
(3)由三角形ABD与三角形CGD全等,利用全等三角形的对应边相等得到AD=DC,确定出三角形ADC为等腰直角三角形,即可求出∠BCA的度数.
解答:(1)证明:∵∠B+∠BAD=90°,∠BAD+∠AGE=90°,
∴∠B=∠AGE,
∵∠AGE=∠CGD,
∴∠B=∠CGD;
(2)证明:在△ABD和△CGD中,
,
∴△ABD≌△CGD(AAS);
(3)解:∵△ABD≌△CGD,
∴AD=DC,
∵∠ADC=90°,
∴∠BCA=45°.
∴∠B=∠AGE,
∵∠AGE=∠CGD,
∴∠B=∠CGD;
(2)证明:在△ABD和△CGD中,
|
∴△ABD≌△CGD(AAS);
(3)解:∵△ABD≌△CGD,
∴AD=DC,
∵∠ADC=90°,
∴∠BCA=45°.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
下列给出的各组线段中,能构成三角形的是( )
| A、5,12,13 |
| B、5,12,7 |
| C、8,9,18 |
| D、3,4,8 |
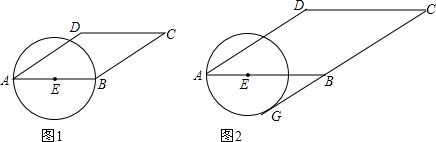
 如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠ACB=∠AED=105°,∠CAD=10°,∠B=∠D=25°,求∠DFB、∠DGB的度数.
如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠ACB=∠AED=105°,∠CAD=10°,∠B=∠D=25°,求∠DFB、∠DGB的度数.