题目内容
14.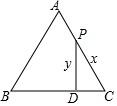 如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )
如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据PD⊥BC于点D,得到∠PDC=90°,根据三角函数的定义得到sin60°=$\frac{y}{x}$=$\frac{\sqrt{3}}{2}$,于是得到结论.
解答 解:∵等边三角形ABC中,∠C=60°,
∵PD⊥BC于点D,
∴∠PDC=90°,
∴sin60°=$\frac{y}{x}$=$\frac{\sqrt{3}}{2}$,
∴y=$\frac{\sqrt{3}}{2}$x,
∴y与x之间的函数关系用图象表示大致是B,
故选B.
点评 本题考查了动点问题的函数图象,等边三角形的性质,三角函数的定义,正确的理解题意是解题的关键.

练习册系列答案
相关题目
4.2016年我省旅游业的总收入为5764亿元,其中5764亿用科学记数法表示为( )
| A. | 5.764×103 | B. | 5.764×1011 | C. | 5764×108 | D. | 0.5764×1012 |
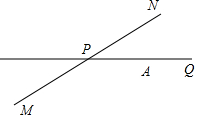 如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160m,假设一拖拉机在公路MN上沿PN方向行驶,周围100m内会受到杂音的影响,如果拖拉机的速度为18km/h,则学校受到影响的时间有多长?
如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160m,假设一拖拉机在公路MN上沿PN方向行驶,周围100m内会受到杂音的影响,如果拖拉机的速度为18km/h,则学校受到影响的时间有多长? 如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形A5B5C5D5,则四边形A5B5C5D5的周长为3.
如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形A5B5C5D5,则四边形A5B5C5D5的周长为3. 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示. 如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)]
如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)]