题目内容
19. 如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)]
如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)](1)试确定b、c的值;
(2)过点C作CD∥x轴,交抛物线于点D,点M为此抛物线的顶点,试确定△MCD的形状.
分析 (1)把(-1,0)、(3,0)代入y=x2+bx+c中,得到关于b、c的二元一次方程组,解即可;
(2)由于CD∥x轴,而且抛物线关于对称轴对称,于是易知l也是CD的垂直平分线,进而可得MC=MD,从而可证.
解答  解:(1)把(-1,0)、(3,0)代入y=x2+bx+c中,得
解:(1)把(-1,0)、(3,0)代入y=x2+bx+c中,得
$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
故b=-2,c=-3;
(2)∵CD∥x轴,抛物线关于对称轴l对称,
∴l⊥x轴,
∴l是CD的垂直平分线,
∴MC=MD,
∵抛物线的解析式为:y=x2-2x-3=(x-1)2-4,
∴点M的坐标为:(1,-4),点C的坐标为:(0,-3),
∴点D的坐标为:(2,-3),
∴CD=2,CM=DM=$\sqrt{2}$,
∴CM2+DM2=CD2,
∴△MCD是等腰直角三角形.
点评 本题考查了待定系数法求函数解析式、二次函数的性质,解题的关键是注意二次函数具有对称性.

练习册系列答案
相关题目
14.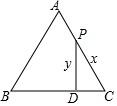 如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )
如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )
 如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )
如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )| A. |  | B. |  | C. |  | D. |  |
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.在以O为原点的平面直角坐标系中,已知点A(3,2)和点B(3,4),则△OAB的面积为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
