题目内容
5. 如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形A5B5C5D5,则四边形A5B5C5D5的周长为3.
如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形A5B5C5D5,则四边形A5B5C5D5的周长为3.
分析 首先证明四边形A1B1C1D1是矩形,求出其周长,再根据规律同理可证四边形A3B3C3D3是矩形,周长为6,四边形A5B5C5D5是矩形,周长为3.
解答 解:∵点A1,D1分别是AB、AD的中点,
∴A1D1是△ABD的中位线
∴A1D1∥BD,A1D1=$\frac{1}{2}$BD,
同理:B1C1∥BD,B1C1=$\frac{1}{2}$BD
∴A1D1∥B1C1,A1D1=B1C1=$\frac{1}{2}$BD,
∴四边形A1B1C1D1是平行四边形.
∵AC⊥BD,AC∥A1B1,BD∥A1D1,
∴A1B1⊥A1D1即∠B1A1D1=90°
∴四边形A1B1C1D1是矩形,
∵A1B1=$\frac{1}{2}$AC=4,A1D1=$\frac{1}{2}$BD=2,
∴四边形A1B1C1D1的周长为12.
同理可证四边形A3B3C3D3是矩形,周长为6,四边形A5B5C5D5是矩形,周长为3.
故答案为3.
点评 本题主要考查了菱形的判定与性质、矩形的判定与性质及三角形的中位线定理(三角形的中位线平行于第三边且等于第三边的一半).解答此题时,需理清菱形、矩形与平行四边形的关系.

练习册系列答案
相关题目
17.下列银行图标中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,正方形AOBC的两边在坐标轴上,D是OB的中点,直线CD的函数关系式为y=2x-6,则△CDE的面积为6.(平方单位)
如图,正方形AOBC的两边在坐标轴上,D是OB的中点,直线CD的函数关系式为y=2x-6,则△CDE的面积为6.(平方单位)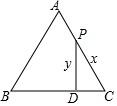 如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )
如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )


