题目内容
9.在边长为4的等边三角形的一边上有任意点P,点P到另两边的距离和为2$\sqrt{3}$.分析 根据等边三角形的性质三边都相等,可知道这点到其他两边的距离之和等于三角形的高.
解答  解:∵从图中可知△ABC的面积=△BPC的面积+△ACP的面积.
解:∵从图中可知△ABC的面积=△BPC的面积+△ACP的面积.
∴$\frac{1}{2}$BD•AD=$\frac{1}{2}$BC•PE+$\frac{1}{2}$AC•PF
∵BD=PF
∴AD=PE+PF
∵AB=4,BD=2
∴AD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
故这点到其他两边的距离之和等于2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查等边三角形的性质,等边三角形三边相等以及根据三角形面积相等求解.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
17.下列银行图标中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
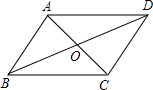 如图,平行四边形ABCD中,对角线AC、BD交于O,不添加任何辅助线,平行四边形满足AC=BD或∠ABC=90°条件时,平行四边形ABCD是矩形.(填一个即可)
如图,平行四边形ABCD中,对角线AC、BD交于O,不添加任何辅助线,平行四边形满足AC=BD或∠ABC=90°条件时,平行四边形ABCD是矩形.(填一个即可)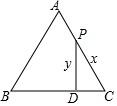 如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )
如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )



 甲、乙两人同时登山,甲、下两人距地面的高度y(单位:米)与登山时间x(单位:分)之间的函数图象如图所示,根据图象提供的信息解答下列问题:
甲、乙两人同时登山,甲、下两人距地面的高度y(单位:米)与登山时间x(单位:分)之间的函数图象如图所示,根据图象提供的信息解答下列问题: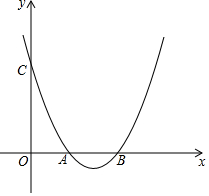 已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).
已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).