题目内容
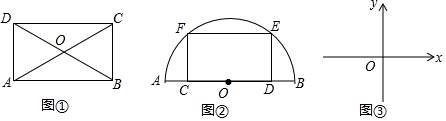
3.定义:一个矩形的两邻边之比为$\sqrt{3}$,则称该矩形为“特比矩形”.(1)如图①,在“特比矩形”ABCD中,$\frac{AB}{BC}$=$\sqrt{3}$,求∠AOD的度数;
(2)如图②,特比矩形CDEF的边CD在半圆O的直径AB上,顶点E、F在半圆上,已知直径AB=$\sqrt{7}$,求矩形CDEF的面积;
(3)在平面直角坐标系xOy中,⊙O的半径为$\sqrt{3}$,点Q的坐标为(q,2$\sqrt{3}$),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围.
分析 (1)由tan∠ACB=$\frac{AB}{BC}$=$\sqrt{3}$,推出∠ACB=60°,由OC=OB,推出△OBC是等边三角形即可解决问题.
(2)如图②中,连接OE,设DE=a,则CD=$\sqrt{3}$a,由Rt△FOC≌Rt△EDO,推出OC=OD=$\frac{\sqrt{3}}{2}$a,在Rt△OED中,OE=$\frac{\sqrt{7}}{2}$,根据OE2=DE2+OD2,列出方程即可解决问题.
(3)取两个特殊点,求出点Q的坐标,再根据对称性即可解决问题.
解答 解:(1)如图①中,
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC=OD=OB,
∴tan∠ACB=$\frac{AB}{BC}$=$\sqrt{3}$,
∴∠ACB=60°,∵OC=OB,
∴△OBC是等边三角形,
∴∠AOD=∠BOC=60°.
(2)如图②中,连接OE,设DE=a,则CD=$\sqrt{3}$a,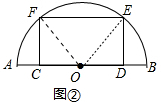
∵CF=DE,OE=OF,∠FCO=∠EDO=90°,
∴Rt△FOC≌Rt△EDO,
∴OC=OD=$\frac{\sqrt{3}}{2}$a,
在Rt△OED中,OE=$\frac{\sqrt{7}}{2}$,
∵OE2=DE2+OD2,
∴$\frac{7}{4}$=a2+$\frac{3}{4}$a2,
∴a=1(负根已经舍弃),
∴DE=1,CD=$\sqrt{3}$,
∴矩形CDEF的面积=1×$\sqrt{3}$=$\sqrt{3}$.
(3)如图③中,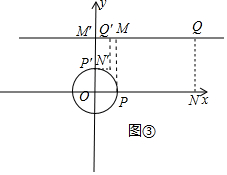
①当点P在x轴正半轴上,易知PM=2$\sqrt{3}$,
∵四边形PMQN是“特比矩形”,
∴MQ=$\sqrt{3}$PM=6,此时Q($\sqrt{3}$+6,2$\sqrt{3}$),
当点P′在y轴的正半轴上时,P′M′=$\sqrt{3}$,
∵四边形PMQN是“特比矩形”,
∴P′M′=$\sqrt{3}$M′Q′,
∴M′Q′=1,
∴Q′(1,2$\sqrt{3}$),
根据对称性、观察图象可知:点Q的横坐标q的取值范围为1≤≤$\sqrt{3}$+6或-$\sqrt{3}$-6≤q≤-1.
点评 本题考查圆综合题、矩形的性质、锐角三角函数、“特比矩形”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用特殊点解决问题,属于中考压轴题.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案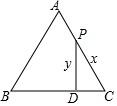 如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )
如图,等边三角形ABC中,在AC边上有一动点P,过P点作PD⊥BC于点D,动点P从C点开始向A点运动,运动到A点停止,设PD为y,PC为x,则y与x之间的函数关系用图象表示大致是( )| A. |  | B. |  | C. |  | D. |  |
| A. |  | B. |  | C. |  | D. |  |
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | x8÷x2=x4 | C. | (2a)3=6a3 | D. | ($\frac{1}{2}$)-1=-$\frac{1}{2}$ |
| A. | 3.82×10-4 | B. | 3.82×10-5 | C. | 3.82×10-6 | D. | 38.2×10-6 |
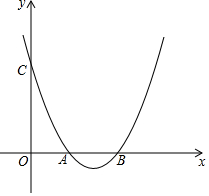 已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).
已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).