题目内容
12.若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是( )| A. | 6 | B. | 8 | C. | 18 | D. | 27 |
分析 多边形的外角和是360°,又有多边形的每个外角都等于40°,所以可以求出多边形外角的个数,进而得到多边形的边数,于是得到结论.
解答 解:这个多边形的边数是:360÷40=9,
∴过该多边形一个顶点的所有对角线条数是9-3=6条,
故选A.
点评 本题考查多边形的外角和,以及多边形外角的个数与其边数之间的相等关系.

练习册系列答案
相关题目
4.“十一”黄金周期间,某景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).
(1)若9月30日的游客人数记为a,则10月2日的游客人数为a+2.4.
(2)黄金周期间,游客人数最多的是10月3日.
(3)若9月30日的游客人数为2万人,门票每人80元,问黄金周期间该景区门票收入是多少元?(用科学记数法表示)
| 日期 | 10月 1日 | 10月 2日 | 10月 3日 | 10月 4日 | 10月 5日 | 10月 6日 | 10月 7日 |
| 人数变化 (单位:万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)黄金周期间,游客人数最多的是10月3日.
(3)若9月30日的游客人数为2万人,门票每人80元,问黄金周期间该景区门票收入是多少元?(用科学记数法表示)
1.一个分子的直径是0.0000000003m,这一数据用科学记数法表示为( )
| A. | 3×10-9m | B. | 3×10-10m | C. | 3×10-11m | D. | 0.3×10-9m |
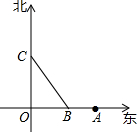 如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.
如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.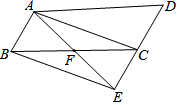 如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE. 如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°,1s后,火箭到达B点,此时测得仰角为45.5°,这枚火箭从点A到点B的平均速度是多少?(结果精确到0.01)
如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°,1s后,火箭到达B点,此时测得仰角为45.5°,这枚火箭从点A到点B的平均速度是多少?(结果精确到0.01)