题目内容
3.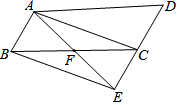 如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.
分析 (1)根据平行四边形的性质得到AB∥CD,AB=CD,然后根据CE=DC,得到AB=EC,AB∥EC,利用“一组对边平行且相等的四边形是平行四边形”判断即可;
(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得出四边形ABEC是矩形,得出∠BAC=90°,由勾股定理求出AC,即可得出平行四边形ABCD的面积.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,BC=AD,
∵CE=DC,
∴AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,
∴BF=CF;
(2)解:∵由(1)知,四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠D,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形,
∴∠BAC=90°,
∵BC=AD=4,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴平行四边形ABCD的面积=AB•AC=2×2$\sqrt{3}$=4$\sqrt{3}$.
点评 此题考查的知识点是平行四边形的判定与性质及矩形的判定,关键是先由平行四边形的性质证三角形全等,然后推出平行四边形通过角的关系证矩形.

练习册系列答案
相关题目
8. 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )| A. | (1345,0) | B. | (1345.5,$\frac{\sqrt{3}}{2}$) | C. | (1345,$\frac{\sqrt{3}}{2}$) | D. | (1345.5,0) |
11.在下列方程中,有实数根的是( )
| A. | x2+3x+5=0 | B. | $\sqrt{2x+1}$+3=0 | C. | $\frac{x}{x-2}$=$\frac{2}{x-2}$ | D. | -x2+x+3=0 |
12.若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是( )
| A. | 6 | B. | 8 | C. | 18 | D. | 27 |
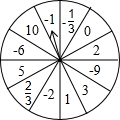 小亮自己设计了一个如图所示的自由转动的均匀的转盘,转盘被等分成12个扇形,每一个扇形里写有一个有理数,自由转动转盘,转盘停止后,分别求下列事件发生的概率:
小亮自己设计了一个如图所示的自由转动的均匀的转盘,转盘被等分成12个扇形,每一个扇形里写有一个有理数,自由转动转盘,转盘停止后,分别求下列事件发生的概率: