题目内容
20．若等边三角形的边长是6，则它的高为（ ）| A． | 3 | B． | 3$\sqrt{2}$ | C． | 3$\sqrt{3}$ | D． | 2$\sqrt{6}$ |
分析 根据等边三角形的三线合一，以及勾股定即可求解．
解答 解：由等边三角形的性质得：
底边的一半是3．再根据勾股定理，得它的高为$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$；
故选：C．
点评 考查了等腰三角形的三线合一性质以及勾股定理，关键是根据等腰三角形的三线合一解答．
练习册系列答案
相关题目
10．关于x的一元二次方程x2-3x-k2=0（k是常数）的根的情况是（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 没有实数根 | D． | 方程根的情况与k的取值有关 |
5．
如图，已知a∥b，且∠2是∠1的2倍，那么∠2的度数为（ ）
如图，已知a∥b，且∠2是∠1的2倍，那么∠2的度数为（ ）| A． | 60° | B． | 90° | C． | 120° | D． | 150° |
已知：⊙O上一点A，作⊙O的内接三角形ABC，使得△ABC为等边三角形．
10．
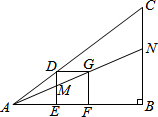如图△ABC中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点．若∠B=90°，AC=5，BC=3，DG=1，则BN的长度为（ ）
如图△ABC中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点．若∠B=90°，AC=5，BC=3，DG=1，则BN的长度为（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{8}{5}$ | D． | $\frac{12}{7}$ |