题目内容
9.已知x1,x2是关于x的方程x2+2(m-2)x+m2+4=0的两个根,是否存在实数m,使x12+x22-x1x2=21成立?若存在,求出m的值;若不存在,请说明理由.分析 先利用判别式的值得到m≤0,再利用根与系数的关系得到x1+x2=-2(m-2),x1x2=m2+4,则利用完全平方公式和整体代入的方法由x12+x22-x1x2=21得到[-2(m-2)]2-3(m2+4)=21,解此方程得m1=17,m2=-1,然后根据m的取值范围确定m的值.
解答 解:存在.
∵△=[-2(m-2)]2-4(m2+4)≥0,
∴m≤0,
根据根与系数的关系得x1+x2=-2(m-2),x1x2=m2+4,
∵x12+x22-x1x2=21,
∴(x1+x2)2-2x1x2-x1x2=21,即(x1+x2)2-3x1x2=21,
∴[-2(m-2)]2-3(m2+4)=21,
整理得m2-16m-17=0,解得m1=17,m2=-1,
而m≤0,
∴m=-1.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.计算出的m的值满足判别式的值大于或等于0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列关于无理数的说法,错误的是( )
| A. | 无理数是实数 | B. | 无理数是无限不循环小数 | ||
| C. | 无理数是无限小数 | D. | 无理数是带根号的数 |
14.下列调查中适宜采用全面调查方式的是( )
| A. | 了解某市的空气质量情况 | |
| B. | 了解某班同学“立定跳远”的成绩 | |
| C. | 了解全市中学生的心理健康状况 | |
| D. | 了解端午节期间大冶市场上的粽子质量情况 |
1.为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
 | 长跑 | 短跑 | 跳绳 | 跳远 |
| 200 | √ | × | √ | √ |
| 300 | × | √ | × | √ |
| 150 | √ | √ | √ | × |
| 200 | √ | × | √ | × |
| 150 | √ | × | × | × |
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
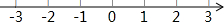 解不等式组$\left\{\begin{array}{l}3x-1<2(x+1)\\-\frac{x}{3}≤\frac{5x}{3}+2\end{array}\right.$并在数轴上表示出解集.
解不等式组$\left\{\begin{array}{l}3x-1<2(x+1)\\-\frac{x}{3}≤\frac{5x}{3}+2\end{array}\right.$并在数轴上表示出解集.