题目内容

4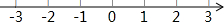．解不等式组$\left\{\begin{array}{l}3x-1＜2（x+1）\\-\frac{x}{3}≤\frac{5x}{3}+2\end{array}\right.$并在数轴上表示出解集．

分析 分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．

解答 解：$\left\{\begin{array}{l}3x-1＜2（x+1）①\\-\frac{x}{3}≤\frac{5x}{3}+2②\end{array}\right.$，由①得，x＜3，由②得，x≥-1，
故不等式组的解集为：-1≤x＜3．
在数轴上表示为：
．

点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．

练习册系列答案
相关题目
14．李莉调查了自己居住小区内30户居民的月人均收入情况，将数据分成4组后，绘制成频数分布直方图，在频数分布直方图中各个小长方表的高的比为1：3：4：2，则第四组数据的频数为（　　）
A．4B．6C．8D．10
15．下列各式中，从左到右变形正确的是（　　）
A．$\frac{b}{a}$=$\frac{{b}^{2}}{{a}^{2}}$B．$\frac{{a}^{2}+{b}^{2}}{a+b}$=a+bC．$\frac{1}{-x+y}$=-$\frac{1}{x-y}$D．$\frac{2y}{2x+y}$=$\frac{y}{x+y}$
12．下列式子中，计算结果为x2+2x-3的是（　　）
A．（x-1）（x+3）B．（x+1）（x-3）C．（x-1）（x-3）D．（x+1）（x+3）
19．有理数a，b，c都不为零，且a+b+c=0，则$\frac{|b+c|}{a}$+$\frac{|a+c|}{b}$+$\frac{|a+b|}{c}$=（　　）
A．1B．±1C．-1D．0
9．已知x1，x2是关于x的方程x2+2（m-2）x+m2+4=0的两个根，是否存在实数m，使x12+x22-x1x2=21成立？若存在，求出m的值；若不存在，请说明理由．
16．解方程组
（1）$\left\{\begin{array}{l}{3x+2y=4}\\{4x+3y=6}\end{array}\right.$
（2）$\left\{\begin{array}{l}{3（x+y）-4（x-y）=13}\\{\frac{x+2y}{7}=2}\end{array}\right.$．
13．若将$\frac{x+y}{xy}$中的字母x、y的值分别扩大为原来的4倍，则分式的值（　　）
A．扩大为原来的4倍B．缩小为原来的$\frac{1}{16}$C．缩小为原来的$\frac{1}{4}$D．不变
14．下列结论正确的是（　　）
A．$-\frac{3}{a}$，b2，-x都是单项式
B．单项式$-\frac{2}{5}m{n^2}$的系数是-$\frac{2}{5}$，次数是3
C．-4a2b，3ab，5是多项式-4a2b+3ab-5的项
D．多项式$-\frac{2}{3}{x^2}-2{x^2}y+3π$是三次二项式，没有常数式

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网