题目内容
3.计算:$\frac{1}{1×5}$+$\frac{1}{5×9}$+$\frac{2}{9×13}$+…+$\frac{1}{2005×2009}$=$\frac{502}{2009}$.分析 先拆项为$\frac{1}{4}$×(1-$\frac{1}{5}$)+$\frac{1}{4}$×($\frac{1}{5}$-$\frac{1}{9}$)+$\frac{1}{4}$×($\frac{1}{9}$-$\frac{1}{13}$)+…+$\frac{1}{4}$×($\frac{1}{2005}$-$\frac{1}{2009}$),再抵消得到原式=$\frac{1}{4}$×(1-$\frac{1}{2009}$),进一步即可求解.
解答 解:$\frac{1}{1×5}$+$\frac{1}{5×9}$+$\frac{2}{9×13}$+…+$\frac{1}{2005×2009}$
=$\frac{1}{4}$×(1-$\frac{1}{5}$)+$\frac{1}{4}$×($\frac{1}{5}$-$\frac{1}{9}$)+$\frac{1}{4}$×($\frac{1}{9}$-$\frac{1}{13}$)+…+$\frac{1}{4}$×($\frac{1}{2005}$-$\frac{1}{2009}$)
=$\frac{1}{4}$×(1-$\frac{1}{2009}$)
=$\frac{1}{4}$×$\frac{2008}{2009}$
=$\frac{502}{2009}$.
故答案为:$\frac{502}{2009}$.
点评 考查了有理数的混合运算,关键是巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.

练习册系列答案
相关题目
11.升国旗时,某同学站在离旗杆底部24m的地方行注目礼,当国旗升到旗杆顶端时,该同学的视线的仰角恰好是45°,若该同学两眼离地面1.5m,则旗杆的高度为( )米.
| A. | 24 | B. | 25.5 | C. | 24$\sqrt{2}$ | D. | 22.5 |
12. 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | $\left\{{\begin{array}{l}{x>1}\\{x>-2}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x≥1}\\{x>-2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x≤1}\\{x<-2}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x<1}\\{x<-2}\end{array}}\right.$ |
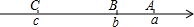 如图,已知A,B,C三点分别对应数轴上的实数a,b,c,化简:|a-b|+|c-b|+|c-a|.
如图,已知A,B,C三点分别对应数轴上的实数a,b,c,化简:|a-b|+|c-b|+|c-a|.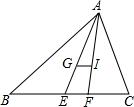 在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.
在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.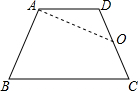 四边形ABCD为梯形,如图所示,其中AD∥BC,O为一腰中点.
四边形ABCD为梯形,如图所示,其中AD∥BC,O为一腰中点.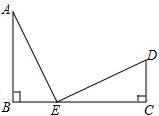 如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.
如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.