题目内容
6.已知y=(m-x)${x}^{{m}^{2}+m-4}$是关于x的二次函数.求:(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,此时当x为何值时,y随x的增大而增大?
(3)当m为何值时,函数有最大值?最大值是多少?此时当x为何值时,y与x的增加而减小?
分析 (1)根据二次函数的定义求出m的值即可解决问题.
(2)运用当二次项系数大于0时,抛物线开口向上,图象有最低点;在对称轴的右侧y随x的增大而增大.
(3)运用当二次项系数小于0时,抛物线开口向下,图象有最高点;在对称轴的右侧y随x的增大而减小.
解答 解:(1)∵函数y=(m-x)${x}^{{m}^{2}+m-4}$是关于x的二次函数,
∴m2+m-4=2,m-1≠0,
解得:m=-3或m=2.
(2)∵m=2,
∴m-1=1,
当m-1=1时,抛物线有最低点,该点坐标为(0,0);
当x>0时,y随x的增大而增大.
(3)∵m=-3,
∴m-1=-4,
当m-1=-4时,函数有最大值,最大值是0;
当x>0时,y随x的增大而减小.
点评 该题主要考查了二次函数的定义及其性质的应用问题;牢固掌握定义及其性质是解题的关键.

练习册系列答案
相关题目
16. 若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )
若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )
 若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )
若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )| A. | 大于b | B. | 小于0 | C. | 小于a | D. | 小于b |
11.升国旗时,某同学站在离旗杆底部24m的地方行注目礼,当国旗升到旗杆顶端时,该同学的视线的仰角恰好是45°,若该同学两眼离地面1.5m,则旗杆的高度为( )米.
| A. | 24 | B. | 25.5 | C. | 24$\sqrt{2}$ | D. | 22.5 |
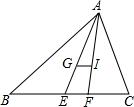 在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.
在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.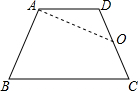 四边形ABCD为梯形,如图所示,其中AD∥BC,O为一腰中点.
四边形ABCD为梯形,如图所示,其中AD∥BC,O为一腰中点.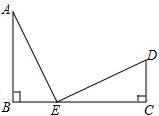 如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.
如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.