题目内容
7．
已知：如图，AB，AC，AD是⊙O的弦．且∠BAC=∠DAC，弦CE∥AB．求证：CE=AD．
分析 连DE，设AD与CE相交于点F，先由平行线的性质得出∠BAC=∠ACE．再由∠BAC=∠CAD得出∠CAD=∠ACE，故AF=CF．根据圆周角定理得出∠D=∠E，故DF=FE，由此可得出结论．
解答 
证明：连DE，设AD与CE相交于点F，
∵AB∥CE，
∴∠BAC=∠ACE．
∵∠BAC=∠CAD，
∴∠CAD=∠ACE，
AF=CF．
∵∠ACE=∠D，∠E=∠CAD，
∴∠D=∠E，
∴DF=FE，
∴AF+DF=CF+EF，即AD=CE．
点评 本题考查的是圆周角定理，根据题意作出辅助线，构造出圆周角是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
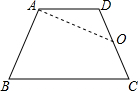四边形ABCD为梯形，如图所示，其中AD∥BC，O为一腰中点．
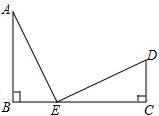如图，E为线段BC上一点，AB⊥BC，△ABE≌△ECD，判断AE与DE的关系，并证明你的结论．
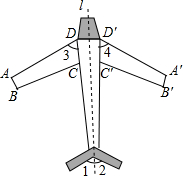如图是轴对称图形．图中直线1是它的对称轴．
12．
把某个不等式组中两个不等式的解集表示在数轴上，如图所示，则这个不等式组可能是（ ）
把某个不等式组中两个不等式的解集表示在数轴上，如图所示，则这个不等式组可能是（ ）| A． | $\left\{{\begin{array}{l}{x＞1}\\{x＞-2}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x≥1}\\{x＞-2}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x≤1}\\{x＜-2}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x＜1}\\{x＜-2}\end{array}}\right.$ |
如图，在边长为2的正方形ABCD中，分别以各顶点为圆心，在正方形内作四条圆弧，使它们所在的圆外切于点E，F，G，H．则图中阴影部分的外围的周长是2π．（结果保留π）