题目内容
17.在一个不透明的袋子中装着四个完全相同的小球,分别标有数字1,-2,3,4,从袋中随机取出一个小球,用小球上的数字作为x(不放回),再取出一个小球,用小球上的数字作为y,确定一个点的坐标为(x,y).(1)请用列表法或者画树状图法表示点的坐标的所有可能结果;
(2)求点位于平面直角坐标系中的第二象限的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)中树状图求得点位于平面直角坐标系中的第二象限的情况,然后直接利用概率公式求解即可求得答案.
解答 解:(1)画树状图得:
则共有12种等可能的结果;
(2)∵点位于平面直角坐标系中的第二象限的有:(-2,1),(-2,3),(-2,4),
∴P(在第二象限)=$\frac{3}{12}$=$\frac{1}{4}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2. 如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )
如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )
 如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )
如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )| A. | ∠A=∠C | B. | BE=DF | C. | AD∥BC | D. | AD=CB |
7.已知(1-m2-n2)(m2+n2)=-6,则m2+n2的值是( )
| A. | 3 | B. | 3或-2 | C. | 2或-3 | D. | 2 |
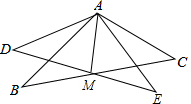 如图,将△ABC绕点A顺时针方向旋转α角度到△ADE的位置,设BC与DE交于M点,连接AM.求证:
如图,将△ABC绕点A顺时针方向旋转α角度到△ADE的位置,设BC与DE交于M点,连接AM.求证: 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.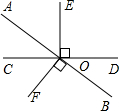 如图,AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,则∠AOE=65°,∠AOC=25°.
如图,AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,则∠AOE=65°,∠AOC=25°.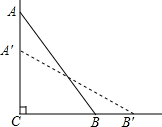 如图,梯子AB斜靠在墙上,梯子的顶端A到地面的距离AC为8m,梯子的底端B距离墙角C为6m.
如图,梯子AB斜靠在墙上,梯子的顶端A到地面的距离AC为8m,梯子的底端B距离墙角C为6m.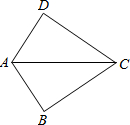 如图,已知AC是∠BAD的平分线,请添加一个条件使△ABC≌△ADC,则需添加的条件是AD=AB(只需写一个正确答案).
如图,已知AC是∠BAD的平分线,请添加一个条件使△ABC≌△ADC,则需添加的条件是AD=AB(只需写一个正确答案).