题目内容
9.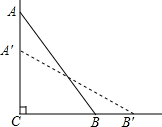 如图,梯子AB斜靠在墙上,梯子的顶端A到地面的距离AC为8m,梯子的底端B距离墙角C为6m.
如图,梯子AB斜靠在墙上,梯子的顶端A到地面的距离AC为8m,梯子的底端B距离墙角C为6m.(1)求梯子AB的长;
(2)当梯子的顶端A下滑2m到点A′时,底端B向外滑动到点B′,求BB′的长.
分析 (1)首先利用勾股定理可得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$,再代入数据进行计算即可;
(2)根据题意可得CA′=8-2=6m,然后利用勾股定理计算出B′C的长度,进而可得BB′的长.
解答 解:(1)∵∠C=90°,AC=8m,BC=6m,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{64+36}$=10m;
(2)∵梯子的顶端A下滑2m,
∴CA′=8-2=6m,
∴CB′=$\sqrt{A′{B′}^{2}-A{′C}^{2}}$=$\sqrt{100-36}$=8(m),
∴BB′=B′C-BC=8-6=2(m).
点评 此题主要考查了勾股定理的应用,关键是正确理解题意,掌握直角三角形中两直角边的平方和等于斜边的平方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.在⊙O中,$\widehat{AB}$所对的圆心角为60°,半径为5cm,则$\widehat{AB}$的长为( )
| A. | $\frac{5}{3}$πcm | B. | $\frac{5}{6}$πcm | C. | $\frac{5\sqrt{3}}{3}$πcm | D. | $\frac{5\sqrt{3}}{6}$πcm |
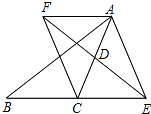 已知,如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF,求证:CF∥AE.
已知,如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF,求证:CF∥AE.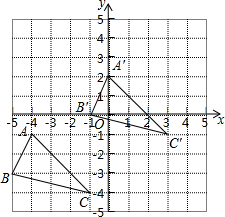 如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2).
如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2).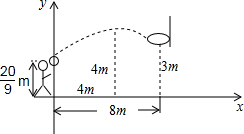 小明跳起投篮,已知球出手时离地面$\frac{20}{9}$m,球与篮筐中心的水平距离为8m,篮筐中心距地面3m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到高度4m,建立如图的平面直角坐标系.
小明跳起投篮,已知球出手时离地面$\frac{20}{9}$m,球与篮筐中心的水平距离为8m,篮筐中心距地面3m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到高度4m,建立如图的平面直角坐标系.