题目内容
2．
如图，AE=CF，∠AFD=∠CEB，添加下列一个条件后，不能判定△ADF≌△CBE的是（ ）| A． | ∠A=∠C | B． | BE=DF | C． | AD∥BC | D． | AD=CB |
分析 如图，首先证明AF=CE；对所给的四个选项逐一判断、解析，可以发现选项D符合题意．
解答 解：添加下列一个条件后，不能判定△ADF≌△CBE的是AD=CB；
理由如下：如图，∵AE=CF，
∴AE+EF=CF+EF，即AF=CE；在△ADF与△CBE中，
∵AF=CE，AD=BC，∠AFD=∠CEB，
即满足有两边和其中一边所对的角相等，
∴这两个三角形不一定全等，
故选D．
点评 该题主要考查了全等三角形的判定方法及其应用问题；应牢固掌握SAS、ASA、AAS、SSS、HL五个判断方法，这是灵活运用的基础和关键．
练习册系列答案
相关题目
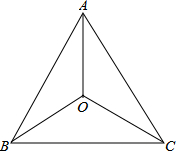如图所示，已知OA平分∠BAC，0B=OC，求证：AB=AC．
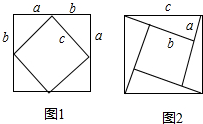勾股定理被誉为千古第一定理长期以来人们对他进行了大量的研究找到了数百种不同的验证方法这些方法不但验证了勾股定理而且丰富了研究数学问题的方法和手段促进了数学的发展请同学们利用图一图二分别证明勾股定理．
10．下列计算：（1）an•an=a2n，（2）a6+a6=a12，（3）c•c5=c5，（4）27+27=28，（5）（3xy3）3=9x3y9 中正确的个数为（ ）
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
7．
如图，数轴上A、B两点分别对应实数a、b，则下列结论正确的是（ ）
如图，数轴上A、B两点分别对应实数a、b，则下列结论正确的是（ ）| A． | a-b＞0 | B． | ab＞0 | C． | a+b＞0 | D． | |a|-|b|＞0 |