题目内容
17.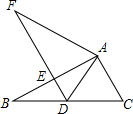 如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )
如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 根据旋转得出∠C=∠FDA,AC=AD,根据直角三角形性质得出AD=DC,求出△ADC是等边三角形,即可求出∠ADC=∠DAC=∠FDB=∠FDA=∠FAB=60°,即可得出选项.
解答 解:∵将△ABC绕点A顺时针旋转后,得到△ADF,
∴∠C=∠FDA,AC=AD,
∵∠BAC=90°,D为BC的中点,
∴AD=DC,
∴∠C=∠DAC,AD=AC=CD,
∴△ADC是等边三角形,
∴∠DAC=∠C=∠ADC=60°,
∴∠FDA=∠C=60°,
∴∠B=30°,∠FDB=180°-60°-60°=60°,
∴∠F=∠B=30°,∠AEF=∠BED=90°,
∴∠FAB=180°-90°-30°=60°,
即∠C=∠ADC=∠DAC=∠FDB=∠FDA=∠FAB=60°,
即和∠C相等的角有5个,
故选A.
点评 本题考查了旋转的性质,直角三角形的性质,等边三角形的性质的应用,能求出△ACD是等边三角形是解此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
6.用一张半径为20的扇形纸片制成一个圆锥(接缝忽略不计),如果圆锥底面的半径为10,那么扇形的圆心角为( )
| A. | 60° | B. | 90° | C. | 135° | D. | 180° |
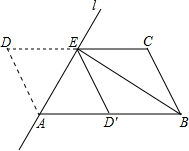 如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=( )
如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=( )
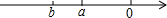 两个实数在数轴上对应点的位置如图所示,则a>b.(填“>”、“<”或“=”)
两个实数在数轴上对应点的位置如图所示,则a>b.(填“>”、“<”或“=”)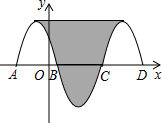 如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.
如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.