题目内容
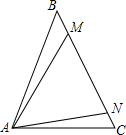 如图,在△ABC中,AB=BC,在BC上分别取点M、N,使MN=NA,若∠BAM=∠NAC,则∠MAC=
如图,在△ABC中,AB=BC,在BC上分别取点M、N,使MN=NA,若∠BAM=∠NAC,则∠MAC=考点:等腰三角形的性质
专题:
分析:先根据AB=BC,∠BAM=∠NAC可知∠BAC=∠BCA=∠BAM+∠NAC+∠MAN=2∠BAM+∠MAN.再由MN=NA可得∠MAN=∠AMN=∠B+∠BAM,故∠BAC=∠BCA=2∠BAM+∠B+∠BAM=∠B+3∠BAM,由三角形内角和定理可知∠B+2(∠B+3∠BAM)=180°,即∠B+2∠BAM=60°,再根据∠B+2(∠MAN+2∠BAM)=180°可知∠MAC=∠NAC+∠MAN=∠BAM+∠MAN,由此可得出结论.
解答:解;∵AB=BC,∠BAM=∠NAC,
∴∠BAC=∠BCA=∠BAM+∠NAC+∠MAN=2∠BAM+∠MAN.
∵MN=NA,
∴∠MAN=∠AMN=∠B+∠BAM,
∴∠BAC=∠BCA=2∠BAM+∠B+∠BAM=∠B+3∠BAM
∴∠B+2(∠B+3∠BAM)=180°,即∠B+2∠BAM=60°
又∵∠B+2(∠MAN+2∠BAM)=180°,即∠B+2∠BAM+2∠BAM+2∠MAN=180°,即2(∠BAM+∠MAN)=180°-60°=120°
∴∠MAC=∠NAC+∠MAN=∠BAM+∠MAN=60°.
故答案为:60.
∴∠BAC=∠BCA=∠BAM+∠NAC+∠MAN=2∠BAM+∠MAN.
∵MN=NA,
∴∠MAN=∠AMN=∠B+∠BAM,
∴∠BAC=∠BCA=2∠BAM+∠B+∠BAM=∠B+3∠BAM
∴∠B+2(∠B+3∠BAM)=180°,即∠B+2∠BAM=60°
又∵∠B+2(∠MAN+2∠BAM)=180°,即∠B+2∠BAM+2∠BAM+2∠MAN=180°,即2(∠BAM+∠MAN)=180°-60°=120°
∴∠MAC=∠NAC+∠MAN=∠BAM+∠MAN=60°.
故答案为:60.
点评:本题考查的是等腰三角形的性质,涉及到三角形内角和定理及三角形外角的性质,熟知等腰三角形的两个底角相等是解答此题的关键.

练习册系列答案
相关题目
 如图,一架长为2.5m的梯子斜靠在竖直的墙上,梯子的底部离墙0.7m,若梯子的顶部滑下0.4m,则梯子的底部向外滑出( )
如图,一架长为2.5m的梯子斜靠在竖直的墙上,梯子的底部离墙0.7m,若梯子的顶部滑下0.4m,则梯子的底部向外滑出( )| A、1.5m | B、0.8m |
| C、0.4m | D、0.9m |
 如图,线段AD到线段BC的运动可能是( )
如图,线段AD到线段BC的运动可能是( )| A、向上平移2格,再向右平移3格 |
| B、向上平移2格,再向左平移1格 |
| C、向上平移1格,再向左平移2格 |
| D、向上平移1格,再向右平移3格 |
将一个正方形剪成n个小正方形,第一次操作按照图1所示,分割出4个正方形,第二次操作按如图2所示,分割出6个正方形,第三次操作按如图3所示,按照上述规律,则第n次操作,正方形的个数为( )
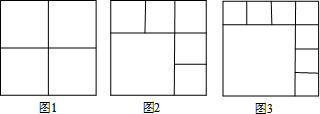

| A、(n+1)2 |
| B、3n+1 |
| C、2n |
| D、2n+2 |
 如图,是一个底面半径为1cm,高度为2πcm的无盖圆柱形玻璃容器,A、B两点在容器顶部一条直径的两端,现有一只小甲虫在容器外A点正下方1cm的M处,要爬到容器内B点正下方距离底部1cm的N处,则这只小甲虫最短爬行的距离是
如图,是一个底面半径为1cm,高度为2πcm的无盖圆柱形玻璃容器,A、B两点在容器顶部一条直径的两端,现有一只小甲虫在容器外A点正下方1cm的M处,要爬到容器内B点正下方距离底部1cm的N处,则这只小甲虫最短爬行的距离是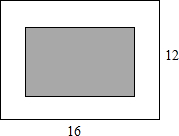 如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽.
如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽.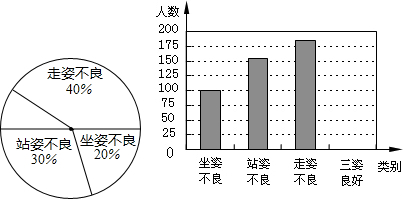
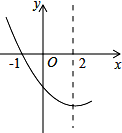 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )