题目内容
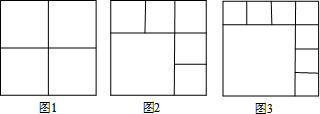
将一个正方形剪成n个小正方形，第一次操作按照图1所示，分割出4个正方形，第二次操作按如图2所示，分割出6个正方形，第三次操作按如图3所示，按照上述规律，则第n次操作，正方形的个数为（ ）
| A、（n+1）2 |
| B、3n+1 |
| C、2n |
| D、2n+2 |
考点：规律型：图形的变化类
专题：
分析：由题意可知：第一次操作按照图1所示，分割出1+1+1×2=4个正方形，第二次操作按如图2所示，分割出1+1+2×2=6个正方形，第三次操作按如图3所示，分割出1+1+2×3=8个正方形，…按照上述规律，则第n次操作，正方形的个数为1+1+2n=2n+2，由此选择得出答案即可．
解答：解：图1分割出1+1+1×2=4个正方形，
图2分割出1+1+2×2=6个正方形，
图3分割出1+1+2×3=8个正方形，
…
则第n次操作，正方形的个数为1+1+2n=2n+2．
故选：D．
图2分割出1+1+2×2=6个正方形，
图3分割出1+1+2×3=8个正方形，
…
则第n次操作，正方形的个数为1+1+2n=2n+2．
故选：D．
点评：此题考查图形的变化规律，找出图形之间的联系，得出数字的运算规律，利用规律解决问题．
练习册系列答案
阅读快车系列答案
相关题目
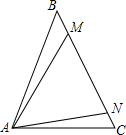如图，在△ABC中，AB=BC，在BC上分别取点M、N，使MN=NA，若∠BAM=∠NAC，则∠MAC=
如图是一个装饰连续旋转闪烁所成的四个图形，照此规律闪烁，第2012次闪烁呈现出来的图形是（ ）
已知二次函数y=x2+bx+c的图象经过点（-4，3）、（-3，0）．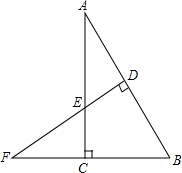
如图，在Rt△ABC中，∠ACB=90°，AB=6，∠A=30°，AB的垂直平分线DE角BC的延长线于F，则FB的长是（ ）