题目内容
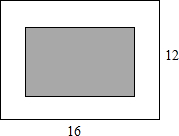 如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽.
如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽.考点:一元二次方程的应用
专题:几何图形问题
分析:设空白部分的宽为x,则地毯的长为(16-2x),地毯的宽为(12-2x),再根据地毯面积占整个会议室地面面积的一半,矩形会议室的面积为16×12,再根据长方形的面积公式,即可列出方程,从而求出符合条件的解.
解答:解:设空白部分的宽为x米,根据题意得出:
(16-2x)(12-2x)=
×16×12,
整理得:x2-14x+24=0,
解得x1=2,x2=12(不合题意,舍去)
则16-2x=16-2×2=12,
12-2x=12-2×2=8.
答:地毯的长与宽分半是12m、8m.
(16-2x)(12-2x)=
| 1 |
| 2 |
整理得:x2-14x+24=0,
解得x1=2,x2=12(不合题意,舍去)
则16-2x=16-2×2=12,
12-2x=12-2×2=8.
答:地毯的长与宽分半是12m、8m.
点评:本题考查了一元二次方程的应用,关键是运用数形结合思想,通过图形可知设空白部分的宽为x,地毯的长和宽就能表示出来,以会议室的面积做为等量关系列出方程求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知线段a=2,b=4,线段c为a,b的比例中项,则c为( )
| A、3 | ||
B、±2
| ||
C、2
| ||
D、
|
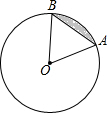 如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为
如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为 在正方形网格中,△ABC的位置如图所示,则tanB的值为
在正方形网格中,△ABC的位置如图所示,则tanB的值为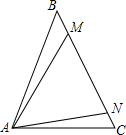 如图,在△ABC中,AB=BC,在BC上分别取点M、N,使MN=NA,若∠BAM=∠NAC,则∠MAC=
如图,在△ABC中,AB=BC,在BC上分别取点M、N,使MN=NA,若∠BAM=∠NAC,则∠MAC=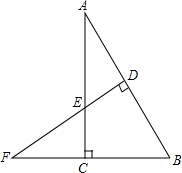 如图,在Rt△ABC中,∠ACB=90°,AB=6,∠A=30°,AB的垂直平分线DE角BC的延长线于F,则FB的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB=6,∠A=30°,AB的垂直平分线DE角BC的延长线于F,则FB的长是( )