题目内容
 如图,一架长为2.5m的梯子斜靠在竖直的墙上,梯子的底部离墙0.7m,若梯子的顶部滑下0.4m,则梯子的底部向外滑出( )
如图,一架长为2.5m的梯子斜靠在竖直的墙上,梯子的底部离墙0.7m,若梯子的顶部滑下0.4m,则梯子的底部向外滑出( )| A、1.5m | B、0.8m |
| C、0.4m | D、0.9m |
考点:勾股定理的应用
专题:
分析:首先根据题意画出图形,利用勾股定理计算出AO的长度,再计算出DO的长度,用DO-OB即可得到梯足移动的距离.
解答: 解:由题意画图形:
解:由题意画图形:
∵AB=2.5m,BO=0.7m,
∴AO=
=2.4(m),
∵AC=0.4m,
∴CO=2m,
∴DO=
=1.5(m),
∴BD=OD-OB=1.5-0.7=0.8(m).
故选B.
 解:由题意画图形:
解:由题意画图形:∵AB=2.5m,BO=0.7m,
∴AO=
| 2.52-0.72 |
∵AC=0.4m,
∴CO=2m,
∴DO=
| CD2-CO2 |
∴BD=OD-OB=1.5-0.7=0.8(m).
故选B.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
已知线段a=2,b=4,线段c为a,b的比例中项,则c为( )
| A、3 | ||
B、±2
| ||
C、2
| ||
D、
|
下列几何体中,三视图既有圆又有长方形的是( )
| A、棱柱 | B、圆柱 | C、圆锥 | D、球 |
 某轮船在O处,测得灯塔A在北偏东40°的方向上,测得灯塔B在南偏东60°的方向上,则∠AOB=
某轮船在O处,测得灯塔A在北偏东40°的方向上,测得灯塔B在南偏东60°的方向上,则∠AOB=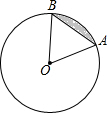 如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为
如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为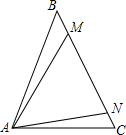 如图,在△ABC中,AB=BC,在BC上分别取点M、N,使MN=NA,若∠BAM=∠NAC,则∠MAC=
如图,在△ABC中,AB=BC,在BC上分别取点M、N,使MN=NA,若∠BAM=∠NAC,则∠MAC= 如图是一个装饰连续旋转闪烁所成的四个图形,照此规律闪烁,第2012次闪烁呈现出来的图形是( )
如图是一个装饰连续旋转闪烁所成的四个图形,照此规律闪烁,第2012次闪烁呈现出来的图形是( )


