题目内容
证明:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
考点:切线长定理,切线的性质
专题:证明题
分析:利用切线的性质结合全等三角形的判定方法得出Rt△OPA≌Rt△OPB即可得出答案.
解答: 已知:PA,PB是⊙O的切线,
已知:PA,PB是⊙O的切线,
求证:PA=PB,∠APO=∠BPO.
证明:连接OA,OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
在Rt△OPA和Rt△OPB中
,
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB,∠APO=∠BPO.
 已知:PA,PB是⊙O的切线,
已知:PA,PB是⊙O的切线,求证:PA=PB,∠APO=∠BPO.
证明:连接OA,OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
在Rt△OPA和Rt△OPB中
|
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB,∠APO=∠BPO.
点评:此题主要考查了切线的性质以及切线长定理的证明,得出Rt△OPA≌Rt△OPB是解题关键.

练习册系列答案
相关题目
一个数的倒数等于-3,那么这个数是( )
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
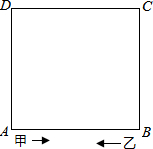 如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米,
如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米, 如图,圆内接四边形对角线AB⊥CD于P,OE⊥AD于E,OE=2,则BC=
如图,圆内接四边形对角线AB⊥CD于P,OE⊥AD于E,OE=2,则BC=