题目内容
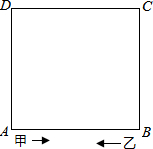 如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米,
如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米,(1)出发后多少分钟时,甲乙两人第一次相遇;
(2)出发后多少分钟时,甲乙两人第一次在正方形的顶点处相遇.
考点:一元一次方程的应用
专题:几何动点问题
分析:(1)设出发后x分钟时,甲乙两人第一次相遇,根据两人行的路程和为40列方程解答即可;
(2)由于两人不是在同一顶点出发,所以两人第一次在同一顶点相遇,需要通过的距离之和等于周长的整数倍再加一条边的长度,即85t=40n+40,其中n是第一次在同一顶点相遇之前通过的周长的个数.
(2)由于两人不是在同一顶点出发,所以两人第一次在同一顶点相遇,需要通过的距离之和等于周长的整数倍再加一条边的长度,即85t=40n+40,其中n是第一次在同一顶点相遇之前通过的周长的个数.
解答:解:(1)设出发后x分钟时,甲乙两人第一次相遇,由题意得
55x+30x=40,
解得:x=
.
答:出发后
分钟时,甲乙两人第一次相遇;
(2)因为两个人的速度之和是85米每分钟,
分钟后两人第一次相遇.如果要两人在顶点相遇,
则:每个人所走的路程均为40的整数倍,且两个人所走路程之和为40+40n(n是指边得条数).
S=40+40n,n为0、1、2、3…n ①
S甲=55t可以被40整除,t为2、4、6…②
S乙=30t也可以被40整除,t为甲方取值即可,
∵S=S甲+S乙,
整理得:55t+30t=40+40n,即:85t=40+40n,
∴n=
③,
由①②③得:当t=8时,两人第一次在顶点相遇.
此时甲走了440米,乙走了2400米,相遇在点D.
答:出发后8分钟时,甲乙两人第一次在正方形的顶点处相遇.
55x+30x=40,
解得:x=
| 8 |
| 17 |
答:出发后
| 8 |
| 17 |
(2)因为两个人的速度之和是85米每分钟,
| 8 |
| 17 |
则:每个人所走的路程均为40的整数倍,且两个人所走路程之和为40+40n(n是指边得条数).
S=40+40n,n为0、1、2、3…n ①
S甲=55t可以被40整除,t为2、4、6…②
S乙=30t也可以被40整除,t为甲方取值即可,
∵S=S甲+S乙,
整理得:55t+30t=40+40n,即:85t=40+40n,
∴n=
| 17t-8 |
| 8 |
由①②③得:当t=8时,两人第一次在顶点相遇.
此时甲走了440米,乙走了2400米,相遇在点D.
答:出发后8分钟时,甲乙两人第一次在正方形的顶点处相遇.
点评:此题考查一元一次方程的实际运用,结合图形,利用行程问题之间的数量关系建立方程是解决问题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,∠BEC=95°,∠C=45°,∠ABE=130°,则AB与CD平行吗?请说明理由.
如图,∠BEC=95°,∠C=45°,∠ABE=130°,则AB与CD平行吗?请说明理由.