题目内容
 已知:如图,以BC为边在矩形ABCD内作等边三角形OBC,连接DO并延长交AB于点E,连接EC,过点C作CF∥DE,交AB的延长线于点F.
已知:如图,以BC为边在矩形ABCD内作等边三角形OBC,连接DO并延长交AB于点E,连接EC,过点C作CF∥DE,交AB的延长线于点F.(1)求证:△ADE≌△BCF;
(2)若OC⊥DE,则四边形DCFE是怎样的特殊四边形?说明理由.
考点:全等三角形的判定与性质,等边三角形的性质,菱形的判定
专题:
分析:(1)易证四边形CDEF为平行四边形,可得CF=DE,即可证明RT△ADE≌RT△BCF,即可解题;
(2)作OG⊥BC,易证G是BC中点,即可求得OG∥AB,可得DE=2DO,易求∠OCD=30°,根据30°角所对直角边是斜边一半的性质可得CD=2DO,即可求得CD=DE,根据邻边相等的平行四边形为菱形即可解题.
(2)作OG⊥BC,易证G是BC中点,即可求得OG∥AB,可得DE=2DO,易求∠OCD=30°,根据30°角所对直角边是斜边一半的性质可得CD=2DO,即可求得CD=DE,根据邻边相等的平行四边形为菱形即可解题.
解答:证明:(1)∵CF∥DE,CD∥AB,
∴四边形CDEF为平行四边形,
∴CF=DE,
在RT△ADE和RT△BCF中,
,
∴RT△ADE≌RT△BCF,(HL);
(2)作OG⊥BC,
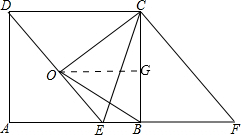
∵△OBC是等边三角形,
∴G是BC中点,
∵AB⊥BC,OG⊥BC,
∴OG∥AB,
∴O是DE中点,即DE=2DO,
∵OC⊥DE,△OBC是等边三角形,
∴∠OCD=30°,
∴CD=2DO,
∴CD=DE,
∴平行四边形CDEF为菱形.
∴四边形CDEF为平行四边形,
∴CF=DE,
在RT△ADE和RT△BCF中,
|
∴RT△ADE≌RT△BCF,(HL);
(2)作OG⊥BC,

∵△OBC是等边三角形,
∴G是BC中点,
∵AB⊥BC,OG⊥BC,
∴OG∥AB,
∴O是DE中点,即DE=2DO,
∵OC⊥DE,△OBC是等边三角形,
∴∠OCD=30°,
∴CD=2DO,
∴CD=DE,
∴平行四边形CDEF为菱形.
点评:本题考查了全等三角形的判定,考查了菱形、平行四边形的判定,考查了平行四边形对边相等的性质,本题中求证RT△ADE≌RT△BCF是解题的关键.

练习册系列答案
相关题目
| cosβ•tanβ |
| sinβ•cotβ |
| A、sinβ | B、cosβ |
| C、tanβ | D、cotβ |
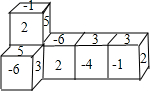 如图是一个由六个小正方体组成的几何体,每个小正方体的六个面上都写有-1,2,3,-4,5,-6,那么图中所有看不见的面上的数字和是( )
如图是一个由六个小正方体组成的几何体,每个小正方体的六个面上都写有-1,2,3,-4,5,-6,那么图中所有看不见的面上的数字和是( )| A、9 | B、8 | C、-15 | D、-13 |
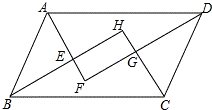 如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论.
如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论. 如图,在数轴上有两点A,B,它们所对应的数分别是a,8,(a<8),把线段AB的中点记为点C.
如图,在数轴上有两点A,B,它们所对应的数分别是a,8,(a<8),把线段AB的中点记为点C. 如图,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?
如图,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?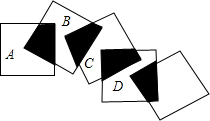 将5个边长都为1cm的正方形按如图所示的样子摆放,点A.B.C.D分别是四个正方形的中心,则图中四块阴影部分的面积的和为
将5个边长都为1cm的正方形按如图所示的样子摆放,点A.B.C.D分别是四个正方形的中心,则图中四块阴影部分的面积的和为