题目内容
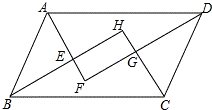 如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论.
如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论.考点:矩形的判定
专题:
分析:由于四边形ABCD是平行四边形,那么AB∥CD,利用平行线的性质可得∠ABC+∠BCD=180°,而BH,CH分别平分∠ABC与∠BCD,则∠HBC=
∠ABC,∠HCB=
∠BCD,那么有∠HBC+∠HCB=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠F=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:四边形EFGH是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=
∠ABC,∠HCB=
∠BCD,
∴∠HBC+∠HCB=
(∠ABC+∠BCD)=
×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠HBC+∠HCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.
点评:本题考查了矩形的判定,平行四边形的性质,角平分线的定义,平行线的性质,难度适中.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
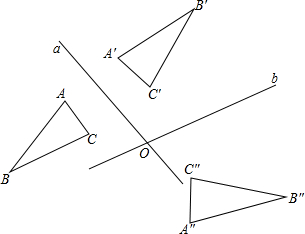 你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到.
你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到. 如图,已知点E、F分别是△ABC中AC、AB边的中点,BE与CF相交于点G,FG=2,则CG的长为
如图,已知点E、F分别是△ABC中AC、AB边的中点,BE与CF相交于点G,FG=2,则CG的长为 小明把手臂水平向前伸直,手持小尺,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A.设小明的手臂长L=50cm,小尺长a=20cm,点D到铁塔底部的距离AD=40m,求铁塔的高度.
小明把手臂水平向前伸直,手持小尺,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A.设小明的手臂长L=50cm,小尺长a=20cm,点D到铁塔底部的距离AD=40m,求铁塔的高度. 已知:如图,以BC为边在矩形ABCD内作等边三角形OBC,连接DO并延长交AB于点E,连接EC,过点C作CF∥DE,交AB的延长线于点F.
已知:如图,以BC为边在矩形ABCD内作等边三角形OBC,连接DO并延长交AB于点E,连接EC,过点C作CF∥DE,交AB的延长线于点F.