题目内容
5.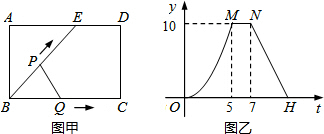 如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:
如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:①当0<t≤5时,y=$\frac{2}{5}$t2
②tan∠ABE=$\frac{3}{4}$
③点H的坐标为(11,0)
④△ABE与△QBP不可能相似.
其中正确的是①②③(把你认为正确结论的序号都填上)
分析 根据图乙可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
解答 ①如图1,过点P作PF⊥BC于点F,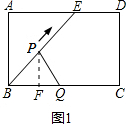
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=$\frac{AB}{BE}=\frac{4}{5}$,
∴PF=PBsin∠PBF=$\frac{4}{5}$t,
∴当0<t≤5时,y=$\frac{1}{2}$BQ•PF=$\frac{1}{2}$t•$\frac{4}{5}$t=$\frac{2}{5}$t2(故②正确);
②又∵从M到N的变化是2,
∴ED=2,
∴AE=AD-ED=5-2=3,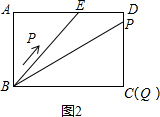
∴tan∠ABE=$\frac{AE}{AB}$=$\frac{3}{4}$,故②正确;
③由图象知,在D点时,出发时间为7s,因为CD=4,所以H(11,0),故③正确;
④当△ABE与△QBP相似时,点P在DC上,如图2所示:
∵tan∠PBQ=tan∠ABE=$\frac{3}{4}$,
∴$\frac{PQ}{BQ}=\frac{3}{4}$,即$\frac{11-t}{5}=\frac{3}{4}$,
解得:t=$\frac{29}{4}$.
故④错误;
故答案为:①②③.
点评 本题考查了二次函数的综合应用及动点问题的函数图象,根据图(2)判断出点P到达点E时,点Q到达点C是解题的关键,也是本题的突破口,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知某山区的平均气温与该山区的海拔的关系见表.
(1)若海拔高度用x(米)表示,平均气温用y(℃)表示,试写出y与x之间的函数关系式;
(2)若某种植物适宜生长在18℃~21℃(包括18℃,也包括21℃)的山区,请问该植物适宜种植在海拔为多少米的山区.
| 海拔/米 | 0 | 100 | 200 | 300 | 400 | … |
| 平均气温/℃ | 24 | 23.4 | 22.8 | 22.2 | 21.6 | … |
(2)若某种植物适宜生长在18℃~21℃(包括18℃,也包括21℃)的山区,请问该植物适宜种植在海拔为多少米的山区.
17. 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )| A. | 140 | B. | 70 | C. | 35 | D. | 24 |
15.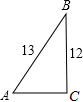 如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
 如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )| A. | sinA=$\frac{12}{13}$ | B. | cosA=$\frac{12}{13}$ | C. | tanA=$\frac{5}{12}$ | D. | tanB=$\frac{12}{5}$ |
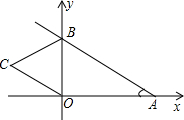 如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.
如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.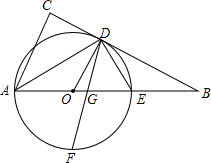 如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG
如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG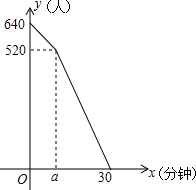 汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:
汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题: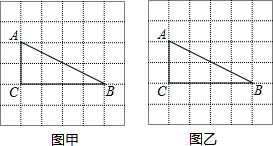
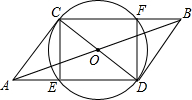 如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.