题目内容
14.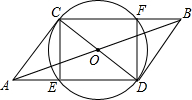 如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.(1)问四边形CEDF是何种特殊四边形?请证明你的结论;
(2)当AC与⊙O相切时,四边形CEDF是正方形吗?请说明理由.
分析 (1)四边形CEDF是矩形,理由是由CD是⊙O的直径,得出∠CFD=∠CED=90°,证出平行四边形ADBC,得出CB∥AD,根据平行线的性质得出∠EDF=90°,即可判断出答案;
(2)在Rt△ACO中,OA=$\sqrt{5}$,OC=1,根据勾股定理求出AC,推出CD=AC=2,∠CDE=45°,进一步推出DE=CE,即可推出答案.
解答 解:(1)四边形CEDF是矩形.
证明:∵CD是⊙O的直径,
∴∠CFD=∠CED=90°,
∵CD⊙O的直径,
∴OC=OD,∵OA=OB,
∴四边形ADBC是平行四边形,
∴CB∥AD,
∴∠CFD+∠EDF=180°,
∴∠EDF=90°,
∴四边形CEDF是矩形.
(2)解:四边形CEDF是正方形.
理由:∵AC是⊙O的切线,CD是直径,
∴∠ACD=90°,
在Rt△ACO中,OA=$\sqrt{5}$,OC=$\frac{1}{2}$CD=1,AC2+12=5,
∴AC=2,
则CD=AC=2,∠CDE=45°,
∴DE=CE,
∴矩形CEDF是正方形.
点评 本题主要考查了对勾股定理,平行四边形的性质和判定,矩形的判定,正方形的判定,切线的性质,平行线的性质等知识点的理解和掌握,综合运用这些性质进行推理是证此题的关键,题型较好,难度适中.

练习册系列答案
相关题目
4.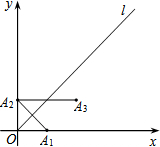 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )| A. | (1007,1008) | B. | (1008,1007) | C. | (1006,1007) | D. | (1007,1006) |
6.下列运算正确的是( )
| A. | (-ab2)3÷(ab2)2=-ab2 | B. | 3a+2a=5a2 | C. | (2a+b)(2a-b)=2a2-b2 | D. | (2a+b)2=4a2+b2 |
4.某商场两天销售甲、乙两种商品的记录如表,由于售货员字迹潦草,无法准确确认第二天的总金额的个位数字,只知道个位数是0或6,并且已知两种商品的销售价仅为整数.
(1)请求出甲、乙两种商品的销售价格各为多少?
(2)若一件甲商品进价为7元,一件乙商品的进价为6元,某天共卖出40件,且两者总利润不低于100元,则至多销售乙商品多少件?
| 总数量(件) | 总金额 | ||
| 甲 | 乙 | ||
| 第一天 | 20 | 10 | 280 |
| 第二天 | 15 | 15 | 27x |
(2)若一件甲商品进价为7元,一件乙商品的进价为6元,某天共卖出40件,且两者总利润不低于100元,则至多销售乙商品多少件?
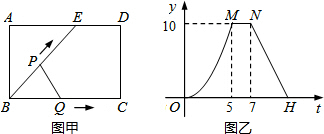 如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:
如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论: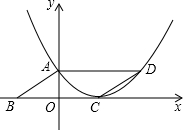 如图,在?ABCD中,BC=6,S?ABCD=12,求抛物线的解析式.
如图,在?ABCD中,BC=6,S?ABCD=12,求抛物线的解析式.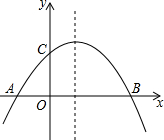 如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.