题目内容
13.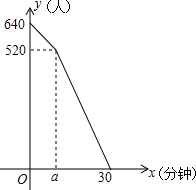 汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:
汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:(1)求a的值;
(2)求泄洪20小时,水库现超过警戒线水量;
(3)若在开始泄洪后15小时内将水库降到警戒线水量,问泄洪一开始至少需要同时打开几个泄洪闸?
分析 (1)首先求得每小时水量的变化情况,然后用水位变化量除每小时水量的变化量即可求得a=10;
(2)根据函数图象可知直线经过点(10,520)和(30,0),从而求得直线的解析式,然后将x=20代入解析式求得y的值即可;
(3)设打开x个泄洪闸,则水库每小时减少水量为(14x-16)万立方米,然后不等式求解即可.
解答 解:(1)(640-520)÷(14×2-16)=10,
∴a=10;
(2)如图所示: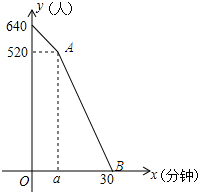
设直线AB的解析式为y=kx+b,将(10,520)和(30,0)代入得:$\left\{\begin{array}{l}{10k+b=520}\\{30k+b=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-26}\\{b=780}\end{array}\right.$
∴直线AB得解析式为y=-26x+780.
将x=20代入得:y=260.、
答:求泄洪20小时,水库现超过警戒线水量为260万m3.
(3)设打开x个泄洪闸.
根据题意得:15×(14x-16)≥640.
解得:x≥$4\frac{4}{21}$
以x取5.
答:泄洪一开始至少需要同时打开5个泄洪闸.
点评 本题主要考查的是一次函数的应用和一元一次不等式的应用,掌握利用待定系数法求一次函数解析式的步骤和方法是解题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
4.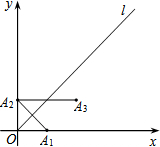 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )| A. | (1007,1008) | B. | (1008,1007) | C. | (1006,1007) | D. | (1007,1006) |
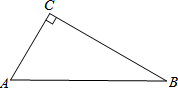 在Rt△ABC中,∠ACB=90°.
在Rt△ABC中,∠ACB=90°.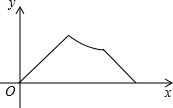 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )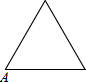
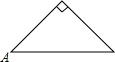
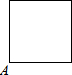
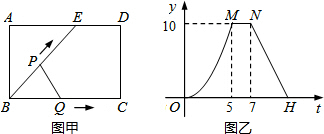 如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:
如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论: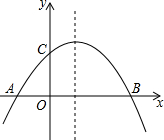 如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.