题目内容
5.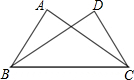 如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)
如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)
分析 根据AAS即可判断①;根据SAS即可判断②;根据ASA即可判断③,根据SSA即可判断④.
解答 解:能证明△ABC≌△DCB的条件是①②③,
理由是:①、∵在△ABC和△DCB中
$\left\{\begin{array}{l}{∠A=∠D}\\{∠ABC=∠DCB}\\{BC=BC}\end{array}\right.$
∴△ABC≌△DCB(AAS);
②、∵在△ABC和△DCB中
$\left\{\begin{array}{l}{AB=DC}\\{∠ABC=∠DCB}\\{BC=BC}\end{array}\right.$
∴△ABC≌△DCB(SAS);
③、∵在△ABC和△DCB中
$\left\{\begin{array}{l}{∠ABC=∠DCB}\\{BC=BC}\\{∠ACB=∠DBC}\end{array}\right.$
∴△ABC≌△DCB(ASA);
④不符合三角形的全等定理;
故答案为:①②③.
点评 本题考查了全等三角形的判定定理的应用,能正确运用判定定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
10.某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
现要配制这种营养食品20千克,要求每千克至少含有9600单位的维生素C.设购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
| 原料 维生素C及价格 | 甲种原料 | 乙种原料 |
| 维生素C(单位/千克) | 600 | 400 |
| 原料价格(元/千克) | 9 | 5 |
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
17.准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
