题目内容
16.某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元.为了扩大销售,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件.(1)若使商场平均每天赢利1200元,则每件衬衫应降价多少元?
(2)若想获得最大利润,每件衬衫应降价多少元?最大利润为多少元?
分析 (1)设每件衬衫应降价x元,根据每件的利润×销售量=平均每天的盈利,列方程求解即可;
(2)根据:总利润=单件利润×销售量列出函数关系式,配方成二次函数顶点式可得函数最值情况.
解答 解:(1)设每件衬衫应降价x元,
则依题意,得:(40-x)(20+2x)=1200,
整理,得,-2x2+60x+800=1200,
解得:x1=10,x2=20,
答:若商场平均每天赢利1200元,每件衬衫应降价10元或20元;
(2)设每件衬衫降价x元时,商场平均每天赢利最多为y,
则y=(40-x)(20+2x)=-2x2+60x+800=-2(x2-30x)+800=-2(x-15)2+1250
∵-2(x-15)2≤0,
∴x=15时,赢利最多,此时y=1250元,
答:每件衬衫降价15元时,商场平均每天赢利最多.
点评 主要考查你对一元二次方程的应用,求二次函数的解析式及二次函数的应用等考点的理解,根据题意准确抓住相等关系式并加以应用是关键.

练习册系列答案
相关题目
7.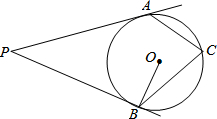 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
4.已知x=$\sqrt{2}-5$,则代数式(x+4)2的值为( )
| A. | 3-2$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 1-$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
6.下列说法中错误的是( )
| A. | 直径是圆中最长的弦 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| C. | 不在同一直线上的三点确定一个圆 | |
| D. | 在同圆或等圆中,能重合的两弧叫做等弧 |
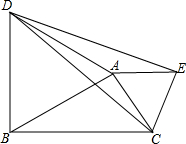 已知,等边△ABD,△ACE,∠BAC=90°,求证:DC=DE.
已知,等边△ABD,△ACE,∠BAC=90°,求证:DC=DE.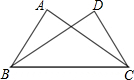 如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)
如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)