题目内容
17.准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 根据题意列出表格,得到所有的可能情况,找到两张牌的牌面数字和为1的情况个数,即可求出所求的概率.
解答 解:根据题意列得:
| 1 | 0 | |
| 1 | 2 | 1 |
| 0 | 1 | 0 |
所以两张牌的牌面数字和为1的概率=$\frac{2}{4}$=$\frac{1}{2}$,
故选C.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
7.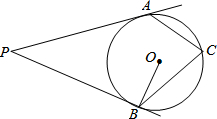 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
2.下列不是二次函数关系的是( )
| A. | y=3x2+4 | B. | y=2x2-x-1 | C. | $y=\frac{8}{x}$ | D. | y=x(x+1) |
6.下列说法中错误的是( )
| A. | 直径是圆中最长的弦 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| C. | 不在同一直线上的三点确定一个圆 | |
| D. | 在同圆或等圆中,能重合的两弧叫做等弧 |
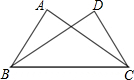 如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)
如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)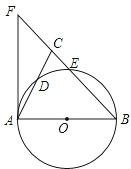 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线与⊙O的切线AF交于点F.