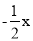题目内容
如图,若∠1与∠2互补,∠2与∠4互补,则( )
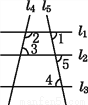
A. l4∥l5 B. l1∥l2 C. l1∥l3 D. l2∥l3
C
【解析】∵∠1与∠2互补，∠2与∠4互补，
∴∠1=∠4(同角的补角相等)，
∴l1∥l3 (内错角相等，两直线平行).
故选：C.
阅读快车系列答案下表是橘子的卖钱额随橘子卖出质量的变化表：
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
卖钱额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
(1)在这个表中反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
(2)如果用x表示橘子的卖出质量，y表示卖钱额，按表中给出的关系，用一个式子把y与x之间的关系表示出来；
(3)当橘子卖出50千克时，预测卖钱额是多少？
（1）质量和卖钱额都是变量，质量是自变量；（2）y＝2x；（3）100元. 【解析】试题分析： 根据表格的第一列确定变量，再结合自变量及因变量的定义确定自变量与因变量； （2）根据表格可知销售单价，由“单价×数量=总价”即可求出y与x的关系； （3）将x=50代入（2）中的关系式，即可求得卖出50千克时的卖钱额. 试题解析： (1) 卖钱额是随卖出质量的变化而变化，所...（9分）一辆出租车从A地出发，在一条东西走向的街道上往返，每次行驶的路程（记向东为正）记录如下（x＞9且x＜26，单位：km）
第一次 | 第二次 | 第三次 | 第四次 |
x |
| x﹣5 | 2（9﹣x） |
（1）说出这辆出租车每次行驶的方向．
（2）求经过连续4次行驶后，这辆出租车所在的位置．
（3）这辆出租车一共行驶了多少路程？
（1）东，西，东，西 ；（2）向东（）千米的位置 ；（）千米
【解析】试题分析：（1）根据数的符号说明即可；
（2）把路程相加，求出结果，看结果的符号即可判断出答案；
（3）求出每个数的绝对值，相加求出即可．
【解析】
（1）第一次是向东，第二次是向西，第三次是向东，第四次是向西．
（2）x+（-x）+（x-5）+2（9-x）=13-x，∵x＞9且x＜26，∴1... 我国作家莫言获得诺贝尔文学奖之后，他的代表作品《蛙》的销售量就比获奖之前增长了180倍，达到2100000册。把2100000用科学记数法表示为( )
A. 0.21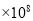
B. 2.1
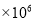C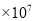. 2.1
D. 21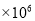
B
【解析】2100000=2.1×106. 如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:
因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(______________),
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF(______________).
垂直的定义;内错角相等,两直线平行
【解析】试题分析：题中已知AB⊥BC，DC⊥BC，根据垂直的定义可得∠ABC=∠BCD=90°，又因为∠1=∠2，由等量减等量，差相等可得∠EBC=∠FCB，观察图形可知，∠EBC与∠FCB是直线BE与CF被直线BC所截的内错角，即可得证.
试题解析：因为AB⊥BC，DC⊥BC（已知），
所以∠ABC=∠BCD=90°（垂直的定义）.
又... 如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
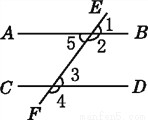
A. ∠1 B. ∠2 C. ∠4 D. ∠5
B
【解析】试题分析：A、∠3与∠1属于同位角，故本选项正确；B、∠3与∠2属于同旁内角，故本选项错误；
C、∠3与∠4于邻补角，故本选项错误；D、∠3与∠5于内错角，故本选项错误．
故选A． 已知：如图：∠1=∠2，∠3+∠4= 180°；确定直线a，c的位置关系，并说明理由；
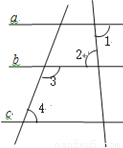
【解析】
a c；
理由：∵∠1=∠2（ ）,
∴ a // ( )；
∵ ∠3+∠4= 180°（ ）,
∴ c // ( )；
∵ a // ,c // ,
∴ // ( )；
答案见解析
【解析】试题分析：本题考查的是同学们对于平行线的判定的运用能力,内错角相等的两条直线平行；同旁内角互补的两条直线平行；平行于同一条直线的两条直线平行.
【解析】
a // c；
理由：∵∠1=∠2（ 已知 ）,
∴ a // b ( 内错角相等，两直线平行 )；
∵ ∠3+∠4= 180°（ 已知 ）,
∴ c // b ( 同旁内角互补， 两直线... 已知△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是70cm和48cm，则△ABC的腰和底边长分别为（ ）
A．24cm和22cm B．26cm和18cm
C．22cm和26cm D．23cm和24cm
C
【解析】
试题分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，然后求出△DBC的周长=AC+BC，再根据两个三角形的周长求出AB，然后BC的值即可．
【解析】
∵AB的垂直平分线交AC于D，
∴AD=BD，
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC，
∵△ABC和△DBC的周长分别是70cm和48cm，
∴... 如图,将△ABC沿BC所在的直线平移到△A'B'C'的位置,则△ABC_______△A'B'C',图中∠A与____,∠B与____,∠ACB与____是对应角.
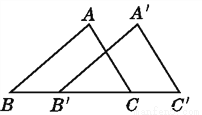
≌ ∠A' ∠A'B'C' ∠C'
【解析】∵△ABC沿BC所在的直线平移到△A'B'C'的位置,
∴△ABC ≌△A'B'C',
∴∠A=∠A'，∠B=∠A'B'C'，∠ACB=∠C'，
∴∠A与∠A'，∠B与∠A'B'C'，∠ACB与∠C'是对应角，
故答案为：≌、∠A'、∠A'B'C'、∠C'