题目内容
如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:
因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(______________),
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF(______________).
垂直的定义;内错角相等,两直线平行
【解析】试题分析：题中已知AB⊥BC，DC⊥BC，根据垂直的定义可得∠ABC=∠BCD=90°，又因为∠1=∠2，由等量减等量，差相等可得∠EBC=∠FCB，观察图形可知，∠EBC与∠FCB是直线BE与CF被直线BC所截的内错角，即可得证.
试题解析：因为AB⊥BC，DC⊥BC（已知），
所以∠ABC=∠BCD=90°（垂直的定义）.
又...
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
若a、b、c为整数，且|a﹣b|19+|c﹣a|95=1，则|c﹣a|+|a﹣b|+|b﹣c|=______．
2
【解析】分两种情况：
①|a-b|=1，|c-a|=0，则c=a，
∴|c-a|+|a-b|+|b-c|=0+|a-b|+|b-a|=0+1+1=2；
②|a-b|=0，|c-a|=1，则a=b，
|c-a|+|a-b|+|b-c|=|c-a|+0+|a-c|=1+0+1=2，
∴|c-a|+|a-b|+|b-c|=2.
故答案为：2． 如图是一个四棱柱和一个六棱锥，它们各有12条棱．
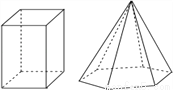
下列棱柱中和九棱锥的棱数相等的是（ ）
A. 五棱柱 B. 六棱柱 C. 七棱柱 D. 八棱柱
B
【解析】∵九棱锥有18条棱，五棱柱有15条棱， 六棱柱有18条棱，七棱柱有21条棱，八棱柱有24条棱，
∴六棱柱的棱数与九棱锥的棱数相等. 下列各数中，负数是 （ ）
A. －(－5) B. －｜－5｜ C. (－5)2 D. －(－5)3．
B
【解析】A. －(－5)=5，是正数；
B. －｜－5｜=-5，是负数；
C. (－5)2 =25，是正数；
D. －(－5)3=-（-125）=125，是正数.
故选B. 如图,若∠1与∠2互补,∠2与∠4互补,则( )
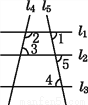
A. l4∥l5 B. l1∥l2 C. l1∥l3 D. l2∥l3
C
【解析】∵∠1与∠2互补，∠2与∠4互补，
∴∠1=∠4(同角的补角相等)，
∴l1∥l3 (内错角相等，两直线平行).
故选：C. 如图,∠1的内错角是( )
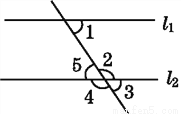
A. ∠2 B. ∠3 C. ∠4 D. ∠5
D
【解析】试题分析：根据内错角位于截线异侧，位于两条被截线之间可知∠1的内错角是∠5．
故选D． 如图，已知在△ABC中，∠C=90°，AB的垂直平分线MN交BC于点D.
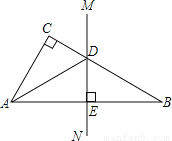
（1）如果∠CAD=20°，求∠B的度数；
（2）如果∠CAB=50°，求∠CAD的度数；
（3）如果∠CAD：∠DAB=1：2，求∠CAB的度数.
（1）∠B＝35°；（2）∠CAD=10°；（3）∠CAB=54°.
【解析】试题分析：（1）根据直角三角形的性质求出∠ADC=70°，根据线段的垂直平分线的性质得到DA=DB，计算即可；
（2）根据直角三角形的性质求出∠B的度数，根据线段的垂直平分线的性质得到DA=DB，计算即可；
（3）设∠CAD=x，根据题意列出方程，解方程即可．
试题解析：（1）∵∠C=90°，∠C... 如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和△BC′F的周长之和为（ ）
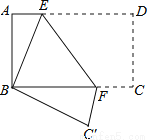
A. 3 B. 4 C. 6 D. 8
C
【解析】试题分析：由折叠特性可得CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，推出∠ABE=∠C′BF，所以△BAE≌△BC′F，根据△ABE和△BC′F的周长=2△ABE的周长求解．
【解析】
将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，
由折叠特性可得，CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC...