题目内容
下表是橘子的卖钱额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
卖钱额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
(1)在这个表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示橘子的卖出质量,y表示卖钱额,按表中给出的关系,用一个式子把y与x之间的关系表示出来;
(3)当橘子卖出50千克时,预测卖钱额是多少?
(1)质量和卖钱额都是变量,质量是自变量;(2)y=2x;(3)100元. 【解析】试题分析: 根据表格的第一列确定变量,再结合自变量及因变量的定义确定自变量与因变量; (2)根据表格可知销售单价,由“单价×数量=总价”即可求出y与x的关系; (3)将x=50代入(2)中的关系式,即可求得卖出50千克时的卖钱额. 试题解析: (1) 卖钱额是随卖出质量的变化而变化,所...
练习册系列答案
相关题目
某大剧场地面的一部分为扇形,观众席的座位数按下列方式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
有下列结论:①排数x是自变量,座位数y是因变量;②排数x是因变量,座位数y是自变量;③y=50+3x;④y=47+3x,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】根据图表可知随着排数的增大,座位数也增大.所以排数x是自变量,座位数y是因变量; 根据图标中的数据可得y=47+3x.故①④正确. 则选:B.研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?
 (1) 红球约占40%,黄球约占60%;(2) 40个.
【解析】分析:(1)根据表格数据可以得到50次摸球实验活动中,出现红球20次,黄球30次,由此即可求出盒中红球、黄球各占总球数的百分比;(2)由题意可知50次摸球实验活动中,出现有记号的球4次,由此可以求出总球数,然后利用(1)的结论即可求出盒中红球.
本题解析: (1)由题意可知,50次摸球试验中,出现红球20次,黄球30次,...
(1) 红球约占40%,黄球约占60%;(2) 40个.
【解析】分析:(1)根据表格数据可以得到50次摸球实验活动中,出现红球20次,黄球30次,由此即可求出盒中红球、黄球各占总球数的百分比;(2)由题意可知50次摸球实验活动中,出现有记号的球4次,由此可以求出总球数,然后利用(1)的结论即可求出盒中红球.
本题解析: (1)由题意可知,50次摸球试验中,出现红球20次,黄球30次,... 如图,关于虚线成轴对称的有( )个.

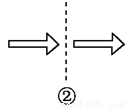
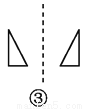
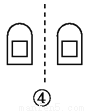
A. 1 B. 2 C. 3 D. 4
 B
【解析】①关于虚线不成轴对称,②关于虚线不成轴对称,③关于虚线不成轴对称,④关于虚线成轴对称,
故选B.
B
【解析】①关于虚线不成轴对称,②关于虚线不成轴对称,③关于虚线不成轴对称,④关于虚线成轴对称,
故选B. 如图,若∠1与∠2互补,∠2与∠4互补,则( )
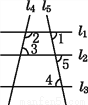
A. l4∥l5 B. l1∥l2 C. l1∥l3 D. l2∥l3
 C
【解析】∵∠1与∠2互补,∠2与∠4互补,
∴∠1=∠4(同角的补角相等),
∴l1∥l3 (内错角相等,两直线平行).
故选:C.
C
【解析】∵∠1与∠2互补,∠2与∠4互补,
∴∠1=∠4(同角的补角相等),
∴l1∥l3 (内错角相等,两直线平行).
故选:C. 

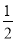 x B. y=
x B. y=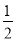 x C. y=-2x D. y=2x
x C. y=-2x D. y=2x