题目内容
17．
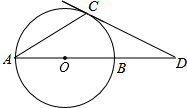如图，AB是⊙O的直径，点C是⊙O上一点，过点C的切线与AB的延长线交于点D，连接AC、CO，若∠A=35°，则∠ADC的度数为（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 55° |
分析 连结OC，如图，根据切线的性质得∠OCD=90°，再利用等腰三角形的性质由OA=OC得到∠A=∠OCA=35°，然后根据三角形内角和计算∠D的度数．
解答 解：连结OC，如图，
∵CD为切线，
∴OC⊥CD，
∴∠OCD=90°，
∵OA=OC，
∴∠A=∠OCA=35°，
∴∠D=180°-∠A-∠ACD=180°-35°-35°-90°=20°．
故选A．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．简记作：见切点，连半径，见垂直．
练习册系列答案
阅读快车系列答案
相关题目
5．
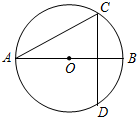如图，AB是⊙O的直径，弦CD垂直平分OB，则∠ACD等于（ ）
如图，AB是⊙O的直径，弦CD垂直平分OB，则∠ACD等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 70° |
12．如表列出了皮球反弹高度和下落高度的数据，其中d表示皮球的下落高度，h表示皮球落地后的反弹高度（单位：cm）
（1）表中反映了哪两个变量之间的关系？哪个是自变量？哪个是函数？
（2）当下落高度是100cm时，皮球的反弹高度是多少？
（2）预测下落高度是90cm时，皮球的反弹高度是多少？
| d | 50 | 80 | 100 | 150 |
| h | 25 | 40 | 50 | 75 |
（2）当下落高度是100cm时，皮球的反弹高度是多少？
（2）预测下落高度是90cm时，皮球的反弹高度是多少？
如图，B，C，E是同一直线上的三个点，四边形ABCD与四边形CEFG都是正方形．连接BG，DE，DE交GF于点H．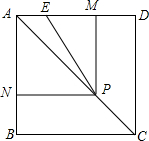
如图，已知正方形ABCD的边长为1，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．