题目内容
10.若不等式8x2+8(a-2)x-a+5>0对任意实数都成立,则实数a的取值范围是$\frac{1}{2}$<a<3.分析 根据根的判别式△<0可求实数a的取值范围.
解答 解:∵不等式8x2+8(a-2)x-a+5>0对任意实数都成立,
∴△=[8(a-2)]2-4×8×(-a+5)<0,
(2a-1)(a-3)<0,
解得$\frac{1}{2}$<a<3.
故实数a的取值范围是$\frac{1}{2}$<a<3.
故答案为:$\frac{1}{2}$<a<3.
点评 此题考查了一元二次不等式,求一元二次不等式的解集实际上是将这个一元二次不等式的所有项移到不等式一侧并进行因式分解分类讨论求出解集.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
18.解方程x-2(x-1)=4,去括号正确的是( )
| A. | x-2x-1=4 | B. | x-2x+2=4 | C. | x-2x-2=4 | D. | x-2x+1=4 |
5.若a2=64,则$\root{3}{a}$的值是( )
| A. | 2 | B. | ±2 | C. | 4 | D. | ±4 |
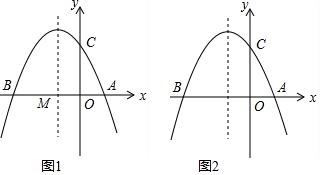 如图1,抛物线y=ax2+bx+6(a≠0)与x轴交于点A(2,0)和点B(-6,0),与y轴交于点C.
如图1,抛物线y=ax2+bx+6(a≠0)与x轴交于点A(2,0)和点B(-6,0),与y轴交于点C.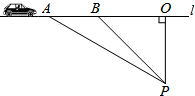 如图,已知测速站P到公路l的距离为40米,一辆汽车在公路l上行驶,测得从点A行驶到点B所用的时间为5秒,并测得∠APO=α,∠BPO=β,计算此车从A到B的平均速度为多少?(已知tanα=$\frac{12}{5}$,sinβ=$\frac{3}{5}$)
如图,已知测速站P到公路l的距离为40米,一辆汽车在公路l上行驶,测得从点A行驶到点B所用的时间为5秒,并测得∠APO=α,∠BPO=β,计算此车从A到B的平均速度为多少?(已知tanα=$\frac{12}{5}$,sinβ=$\frac{3}{5}$) 如图,在平面直角坐标系中,将△ABC点C顺时针旋转90°后得则△A′B′C′.
如图,在平面直角坐标系中,将△ABC点C顺时针旋转90°后得则△A′B′C′. 如图,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠1=∠2,求∠BPC的度数.
如图,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠1=∠2,求∠BPC的度数.