题目内容
1.已知方程组$\left\{\begin{array}{l}{ax+5y=4}\\{5x+y=3}\end{array}\right.$,与方程组$\left\{\begin{array}{l}{x-2y=5}\\{5x+by=1}\end{array}\right.$,的解相同,求a,b的值.分析 联立两方程组中不含a与b的方程求出x与y的值,即可确定出a与b的值.
解答 解:联立得:$\left\{\begin{array}{l}{5x+y=3①}\\{x-2y=5②}\end{array}\right.$,
①×2+②得:11x=11,即x=1,
把x=1代入②得:y=-2,
把x=1,y=-2代入得:$\left\{\begin{array}{l}{a-10=4}\\{5-2b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=14}\\{b=3}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
12.下列对正方形的描述错误的是( )
| A. | 正方形的四个角都是直角 | B. | 正方形的对角线互相垂直 | ||
| C. | 邻边相等的矩形是正方形 | D. | 对角线相等的平行四边形是菱形 |
9.单项式2x2y2的次数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
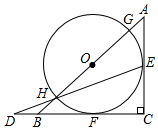 如图,△ABC是等腰直角三角形,AC=BC=2a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为(1+$\sqrt{2}$)a.
如图,△ABC是等腰直角三角形,AC=BC=2a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为(1+$\sqrt{2}$)a. 画出图中几何体的三视图.
画出图中几何体的三视图. 如图,已知∠1=72°,∠4=110°,∠3=70°,则∠2=72°.
如图,已知∠1=72°,∠4=110°,∠3=70°,则∠2=72°.