题目内容
2.供给侧改革就是压产量、去库存、促销售.武侯区某轿车销售公司为龙泉工业区代销A款轿车,为了吸引购车族,销售公司打出降价牌,今年5月份A款轿车每辆售价比去年同期每辆售价低1万元,如果卖出相同数量的A款轿车,去年的销售额为100万元,今年销售额只有90万元.(1)今年5月份A款轿车每辆售价为多少元?
(2)为了增加收入,该轿车公司决定再为龙泉工业区代销B款轿车.已知A款轿车每辆进价为7.5万元,B款轿车每辆进价为6万元,公司预计用不多于105万元的资金购进这两款轿车共15辆,但A款轿车不少于6辆,试问共有几种进货方案?
(3)在(2)的条件下,B款轿车每辆售价为8万元,为打开B款轿车的销路,公司决定每售出一辆B款轿车,返还顾客现金a(0<a≤1)万元.假设购进的15辆车能够全部卖出去,试讨论采用哪种进货方案可以使该轿车销售公司卖出这15辆车后获得最大利润?
分析 (1)求单价,总价明显,应根据数量来列等量关系.等量关系为:今年的销售数量=去年的销售数量.
(2)关系式为:99≤A款汽车总价+B款汽车总价≤105.
(3)方案获利相同,说明与所设的未知数无关,让未知数x的系数为0即可;多进B款汽车对公司更有利,因为A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,所以要多进B款.
解答 解:(1)设今年5月份A款汽车每辆售价x万元.根据题意得:
$\frac{100}{x+1}$=$\frac{90}{x}$,
解得:x=9,
经检验知,x=9是原方程的解.
所以今年5月份A款汽车每辆售价9万元.
(2)设A款汽车购进y辆.则B款汽车每辆购进(15-y)辆.根据题意得:$\left\{\begin{array}{l}{7.5y+6(15-y)≤105}\\{y≥6}\end{array}\right.$
解得:6≤y≤10,
所以有5种方案:
方案一:A款汽车购进6辆;B款汽车购进9辆;
方案二:A款汽车购进7辆;B款汽车购进8辆;
方案三:A款汽车购进8辆;B款汽车购进7辆;
方案四:A款汽车购进9辆;B款汽车购进6辆;
方案五:A款汽车购进10辆;B款汽车购进5辆.
(3)设利润为W则:W=(8-6)×(15-y)-a(15-y)+(9-7.5)y
=30-2y-a(15-y)+1.5y
=30-a(15-y)-0.5y
=(a-0.5)y+30-15a.
①当a=0.5时,5种方案利润一样.
②当a>0.5时,y=10时,利润最大,此时方案五利润最大.
③当a<0.5时,y=6时,利润最大,此时方案一利润最大.
点评 本题考查一次函数的应用、分式方程、一元一次不等式组等知识,找到合适的等量关系及不等关系是解决问题的关键.

| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y | … | -2 | -3 | -6 | 6 | 3 | 2 | … |
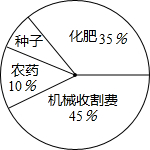 南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图:
南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图:| 每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
| 310元 | 130千克 | 5元/千克 | 500000亩 |
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2014年南县全县农民冬种油菜的总获利为多少元?(结果用科学记数法表示)
 如图,已知∠1=72°,∠4=110°,∠3=70°,则∠2=72°.
如图,已知∠1=72°,∠4=110°,∠3=70°,则∠2=72°.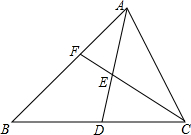 如图△ABC中,AD为中线,求证:AE:ED=2AF:FB.
如图△ABC中,AD为中线,求证:AE:ED=2AF:FB.