题目内容
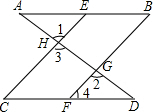
16.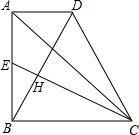 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.(1)求证:BD⊥EC.
(2)连接DE交AC于点M,求证:AM2=$\frac{1}{2}$EH•DC.
分析 (1)先证明△DAB≌△EBC,于是得到∠ADB=∠BEC,由AD∥BC,可知∠ADB=∠DBC,故此∠∠BEC=∠HBC,然后由∠BEC+∠ECB=90°,可得到∠HBC+BCH=90°,故此可知BD⊥EC;
(2)连接AH.先证明△AED、△ABC、△AEM为等腰直角三角形,从而得到AE=$\sqrt{2}$AM,由等腰三角形三线合一的性质可证明AC是ED的垂直平分线,故此DC=EC,然后再证明△AEH∽△CEA,由相似三角形的性质可得到AM2=$\frac{1}{2}$EH•DC.
解答 (1)证明:∵E是AB的中点,且AD=$\frac{1}{2}$AB,
∴AE=AD.
在△DAB和△EBC中,
$\left\{\begin{array}{l}{AD=EB}\\{∠DAB=∠EBC=90°}\\{AB=BC}\end{array}\right.$,
∴△DAB≌△EBC.
∴∠ADB=∠BEC.
∵AD∥BC,
∴∠ADB=∠DBC.
∴∠∠BEC=∠HBC.
∵∠BEC+∠ECB=90°,
∴∠HBC+BCH=90°.
∴D⊥EC.
(2)解:如图所示,连接AH.
∵E是AB的中点,且AD=$\frac{1}{2}$AB,
∴AE=AD.
∵AB=BC,∠ABC=90°,
∴∠BAC=45°.
∴AC平分∠EAD.
∴AM⊥DE,ME=DM.
∴DC=EC.
∵在Rt△AEM中,∠EAM=45°
∴AE=$\sqrt{2}AM$.
∵EC⊥BD,
∴∠EHD=90°.
∴∠EAD+∠EHD=180°.
∴A、E、H、D四共圆.
∴∠AHE=∠ADE=45°.
∴∠AHE=∠EAC=45°.
又∵∠AEH=∠CEA,
∴△AEH∽△CEA.
∴$\frac{AE}{EH}=\frac{EC}{AE}$,即$\frac{\sqrt{2}AM}{EH}=\frac{DC}{\sqrt{2}AM}$.
∴AM2=$\frac{1}{2}EH•DC$.
点评 本题主要考查的是相似三角形的性质和判定、全等三角形的性质和判定、四点共圆的条件、圆周角定理、等腰直角三角形的性质和判定,连接AH,证明△AEH∽△CEA是解题的关键.

 金钥匙试卷系列答案
金钥匙试卷系列答案 如图折叠一张长方形纸片,BC,BD为折痕,则∠CBD的度数为( )
如图折叠一张长方形纸片,BC,BD为折痕,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
 如图,O是△ABC内一点,BO=CO,∠ABO=∠ACO,求证:AO平分∠BAC.
如图,O是△ABC内一点,BO=CO,∠ABO=∠ACO,求证:AO平分∠BAC.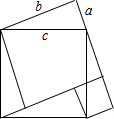 (1)画出“弦图”,并利用“弦图”证明勾股定理.
(1)画出“弦图”,并利用“弦图”证明勾股定理.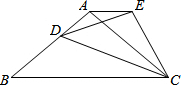 如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:
如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证: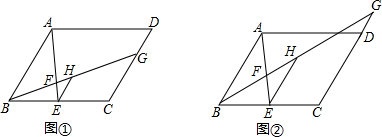
 把下面的说理过程补充完整:
把下面的说理过程补充完整: 如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,则图中等腰三角形的个数是6.
如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,则图中等腰三角形的个数是6.