题目内容
7.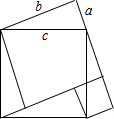 (1)画出“弦图”,并利用“弦图”证明勾股定理.
(1)画出“弦图”,并利用“弦图”证明勾股定理.(2)如图,是4个完全相同的直角三角形适当拼接后形成的图形,这些直角三角形的两直角边分别为a、b,斜边为c.请利用这个图形验证勾股定理.
分析 (1)先证出四边形ABDE和四边形GHMC是正方形,分别用两种方法求出大正方形的面积,即可得出答案.
(2)验证勾股定理,根据已知条件,可通过求该图形的面积列出等式,化简即可得到勾股定理的形式.
解答 (1)解:如图所示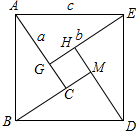 :
:
∵△ABC、△BMD、△DHE、△AGE是全等的四个直角三角形,
∴AE=DE=BD=AB,∠EAG+∠BAC=∠EAG+∠AEG=180°-90°=90°,
∴四边形ABDE是正方形,
∵∠AGE=∠EHD=∠BMD=∠ACB=90°,
∴∠HGC=90°,
∵GH=HM=CM=CG=b-a,
∴四边形GHMC是正方形,
∴大正方形的面积是c×c=c2,
大正方形的面积也可以是:4×$\frac{1}{2}$ab+(b-a)2=2ab+a2-2ab+b2=a2+b2,
∴a2+b2=c2,
即在直角三角形中,两直角边(a、b)的平方和等于斜边(c)的平方.
(2)证明:该图形的面积,有两种求法:
一种为正方形的面积+两个直角三角形的面积;
一种为两正方形的面积+两直角三角形的面积,
根据两种求法的面积相等可得:c2+2×$\frac{1}{2}$ab=b2+2×$\frac{1}{2}$ab+a2,
化简得,a2+b2=c2.
点评 本题考查了勾股定理的证明,考查了学生对组合图形的认识和勾股定理证明的认识,题目比较好,难度不大.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
17. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )| A. | 60° | B. | 55° | C. | 50° | D. | 无法计算 |
2.已知:ab≠0,且M=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|ab|}{ab}$,当a、b取不同的值时,M有( )
| A. | 唯一确定的值 | B. | 2种不同的取值 | C. | 3种不同的取值 | D. | 4种不同的取值 |
19.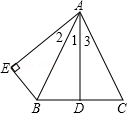 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
(1)求证:AD=AE;
(2)求证:∠DAE=∠BAC;
(2)若∠2=30°,试判断△ABC的形状,并说明理由.
 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.(1)求证:AD=AE;
(2)求证:∠DAE=∠BAC;
(2)若∠2=30°,试判断△ABC的形状,并说明理由.
17.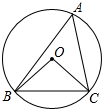 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
 已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法)
已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法) 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.