题目内容
5. 如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,则图中等腰三角形的个数是6.
如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,则图中等腰三角形的个数是6.
分析 根据已知条件和三角形的内角和得到∠BAC=120°,∠B=30°,∠C=30°,由于AD,AE将∠BAC三等分,于是求得∠BAD=∠DAE=∠EAC=30°,根据外角的性质和三角形的内角和得到∠ADE=∠AED=∠BAE=∠CAD=60°,于是得到结论.
解答 解:∵∠BAC:∠B:∠C=3:1:1,∠BAC+∠B+∠C=180°,
∴∠BAC=108°,∠B=36°,∠C=36°,
∵AD,AE将∠BAC三等分,
∴∠BAD=∠DAE=∠EAC=36°,
∴∠ADE=∠AED=∠BAE=∠CAD=72°,
∴AD=BD,AD=AE,AE=CE,AB=AC,AB=BE,AC=CD,
∴△ABD,△ADE,△AEC,△ABC,△ABE,△ACD是等腰三角形,
∴图中等腰三角形的个数是6,
故答案为:6.
点评 本题考查了等腰三角形的判定和性质,解题的关键是求出每个角的度数,根据等角对等边即可判断.

练习册系列答案
相关题目
20.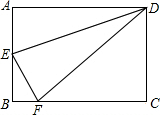 如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )
如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )
 如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )
如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )| A. | 10cm | B. | 9cm | C. | 8cm | D. | 7cm |
10.已知函数:①y=3x-1;②y=3x2-1;③y=-20x2;④y=x2-6x+5,其中是二次函数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.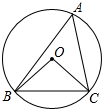 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
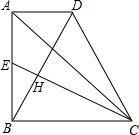 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.