题目内容
4. 如图折叠一张长方形纸片,BC,BD为折痕,则∠CBD的度数为( )
如图折叠一张长方形纸片,BC,BD为折痕,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
分析 由折叠的性质,即可得:∠ABC=∠A′BC,∠EBD=∠E′BD,然后由平角的定义,即可求得∠A′BC+∠E′BD=90°,则可求得∠CBD的度数.
解答 解:根据折叠的性质可得:∠ABC=∠A′BC,∠EBD=∠E′BD,
∵∠ABC+∠A′BC+∠E′BD+∠EBD=180°,
∴2∠A′BC+2∠E′BD=180°.
∴∠A′BC+∠E′BD=90°.
∴∠CBD=90°.
故选:C.
点评 此题考查了折叠的性质与平角的定义,解题的关键是掌握翻折的性质.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
14.已知关于x的一元二次方程x2+bx+a=0有一个非零根-a,则a-b的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
19.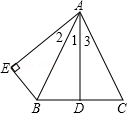 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
(1)求证:AD=AE;
(2)求证:∠DAE=∠BAC;
(2)若∠2=30°,试判断△ABC的形状,并说明理由.
 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.(1)求证:AD=AE;
(2)求证:∠DAE=∠BAC;
(2)若∠2=30°,试判断△ABC的形状,并说明理由.
9.抛物线y=-2x2-1的对称轴是( )
| A. | 直线x=$\frac{1}{2}$ | B. | 直线x=-$\frac{1}{2}$ | C. | y轴 | D. | 直线x=2 |
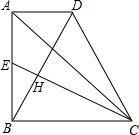 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.