题目内容
8. 把下面的说理过程补充完整:
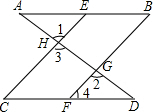
把下面的说理过程补充完整:已知:如图,直线AD与AB、CD相交于A、D两点,EC、BF与AB、CD相交于E、C、B、F,如果∠1=∠2,∠B=∠C,求证:∠A=∠D.
证明:∵∠1=∠2(已知),∠1=∠3(对顶角相等)
∴∠2=∠3
∴CE∥BF(同位角相等,两直线平行)
∴∠C=∠4(两直线平行,同位角相等)
又∵∠B=∠C(已知),
∴∠B=∠4,
∴AB∥CD(内错角相等,两直线平行)
∴∠A=∠D(两直线平行,内错角相等)
分析 要证明∠A=∠D,只需证明AB∥CD.根据已知的∠1=∠2和对顶角相等,可以得到BF∥CE.再根据平行线的性质和∠B=∠C,就可得到∠C=∠AEC,从而完成证明.
解答 证明:∵∠1=∠2(已知),∠1=∠3(对顶角相等)
∴∠2=∠3
∴CE∥BF(同位角相等,两直线平行)
∴∠C=∠4(两直线平行,同位角相等)
又∵∠B=∠C,(已知),
∴∠B=∠4,
∴AB∥CD(内错角相等,两直线平行)
∴∠A=∠D(两直线平行,内错角相等)
故答案为:对顶角相等,CE∥BF,同位角相等,两直线平行,两直线平行,同位角相等,∠B=∠C,内错角相等,两直线平行,两直线平行,内错角相.
点评 本题考查了平行线的判定和性质,对顶角相等,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
相关题目
19.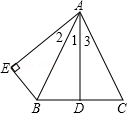 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
(1)求证:AD=AE;
(2)求证:∠DAE=∠BAC;
(2)若∠2=30°,试判断△ABC的形状,并说明理由.
 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.(1)求证:AD=AE;
(2)求证:∠DAE=∠BAC;
(2)若∠2=30°,试判断△ABC的形状,并说明理由.
20.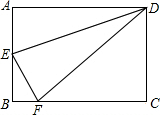 如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )
如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )
 如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )
如图,长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5cm,BF=3cm,则CD的长度是( )| A. | 10cm | B. | 9cm | C. | 8cm | D. | 7cm |
17.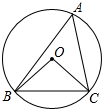 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
 已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法)
已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法)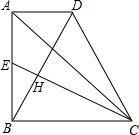 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.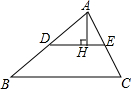 如图,在△ABC中,点D、E分别是AB、AC的中点,AH⊥DE于点H,已知AH=3,BC=10,则S△ABC=30.
如图,在△ABC中,点D、E分别是AB、AC的中点,AH⊥DE于点H,已知AH=3,BC=10,则S△ABC=30.