题目内容
6. 如图,O是△ABC内一点,BO=CO,∠ABO=∠ACO,求证:AO平分∠BAC.
如图,O是△ABC内一点,BO=CO,∠ABO=∠ACO,求证:AO平分∠BAC.
分析 根据等腰三角形的性质求出∠OBC=∠OCB,求出∠ABC=∠ACB,求出AB=AC,根据SSS推出△AOB≌△AOC,根据全等三角形的性质得出∠BAO=∠CAO即可.
解答 证明:∵BO=CO,
∴∠OBC=∠OCB,
∵∠ABO=∠ACO,
∴∠ABO+∠OBC=∠ACO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
在△AOB和△AOC中
$\left\{\begin{array}{l}{AB=AC}\\{AO=AO}\\{OB=OC}\end{array}\right.$
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO,
即AO平分∠BAC.
点评 本题考查了等腰三角形的性质和判定,全等三角形的性质和判定的应用,能求出△AOB≌△AOC是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列说法正确的是( )
| A. | $\sqrt{81}$的平方根是3 | B. | ±$\frac{8}{7}$是1$\frac{15}{49}$的平方根 | ||
| C. | -3是27的负立方根 | D. | (-4 )2的平方根是-4 |
17. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )| A. | 60° | B. | 55° | C. | 50° | D. | 无法计算 |
14.已知关于x的一元二次方程x2+bx+a=0有一个非零根-a,则a-b的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
11.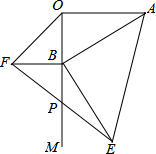 如图,AO⊥OM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是( )
如图,AO⊥OM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是( )
 如图,AO⊥OM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是( )
如图,AO⊥OM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是( )| A. | 3.6 | B. | 4 | ||
| C. | 4.8 | D. | PB的长度随B点的运动而变化 |
 已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法)
已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法)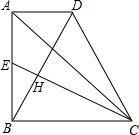 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,且AD=$\frac{1}{2}$AB.