题目内容
6.下列关系式中,正确的是( )| A. | (a+b)2=a2-2ab+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)(-a+b)=b2-a2 | D. | (a+b)(-a-b)=a2-b2 |
分析 A、B符合完全平方公式;C符合平方差公式;D先将原式变形为-(a+b)(a+b)=-(a+b)2,然后利用平方差公式计算.
解答 解:A.(a+b)2=a2+2ab+b2,故A错误;
B..(a-b)2=a2-2ab+b2,故B错误;
C.原式=(b+a)(b-a)=b2-a2,故C正确;
D.原式-(a+b)(a+b)=-(a+b)2=-(a2+2ab+b2)=-a2-2ab-b2,故D错误.
故选:C.
点评 本题主要考查的是平方差公式和完全平方公式的应用,熟记平方差公式和完全平方公式是解题的关键.

练习册系列答案
相关题目
17. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③-1≤a≤-$\frac{2}{3}$;④4ac-b2>8a;
其中正确的结论是( )
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③-1≤a≤-$\frac{2}{3}$;④4ac-b2>8a;
其中正确的结论是( )
| A. | ①③④ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
15.下列图案中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.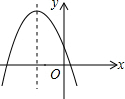 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
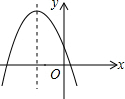 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )| A. | 一、三象限 | B. | 一、二象限 | C. | 二、三象限 | D. | 二、四象限 |
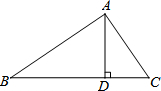 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.
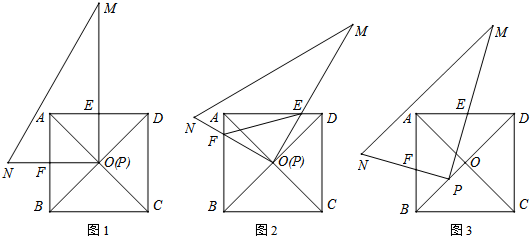
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.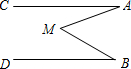 如图,AC∥DB,∠A=20°,∠B=30°,那么∠AMB=50°.
如图,AC∥DB,∠A=20°,∠B=30°,那么∠AMB=50°.