题目内容
4.在同一平面直角坐标系中,若一次函数y=-x+1与y=2x+4的图象交于点M,则点M的坐标为( )| A. | (-1,-2) | B. | (-1,2) | C. | (2,1) | D. | (-2,1) |
分析 根据两直线的交点问题,通过解方程组$\left\{\begin{array}{l}{y=-x+1}\\{y=2x+4}\end{array}\right.$即可得到M点坐标.
解答 解:解方程组$\left\{\begin{array}{l}{y=-x+1}\\{y=2x+4}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,
所以M点的坐标为(-1,2).
故选B.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
15.已知△ABC∽△DEF,且相似比为2:3,则△ABC与△DEF的对应高之比为( )
| A. | 2:3 | B. | 3:2 | C. | 4:9 | D. | 9:4 |
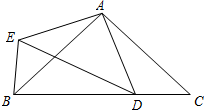 已知:如图,在△ABC中,点D在边BC上,AB=AC,∠DAE=∠BAC,AE=AD,联结DE、BE.
已知:如图,在△ABC中,点D在边BC上,AB=AC,∠DAE=∠BAC,AE=AD,联结DE、BE.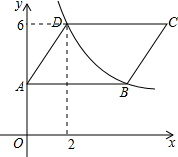 如图,平行四边形ABCD的顶点B,D都在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )
如图,平行四边形ABCD的顶点B,D都在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( ) 我国古代有这样一道数学题:“枯木一根直立地上,高2丈,周3尺,有葛藤自根缠绕而上,5周而达其顶.问葛藤之长几何?”这里1丈=10尺,葛藤之长指它的最短长度.解题时,枯木视为圆柱体(如图所示)周3尺指圆柱体底面周长3尺.那么葛藤的长是25尺.
我国古代有这样一道数学题:“枯木一根直立地上,高2丈,周3尺,有葛藤自根缠绕而上,5周而达其顶.问葛藤之长几何?”这里1丈=10尺,葛藤之长指它的最短长度.解题时,枯木视为圆柱体(如图所示)周3尺指圆柱体底面周长3尺.那么葛藤的长是25尺.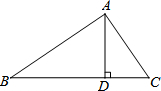 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.