题目内容
 已知AD是△ABC的高,△ABC外接圆的半径为R,
已知AD是△ABC的高,△ABC外接圆的半径为R,(1)当△ABC为锐角三角形时,求证:AB•AC=2AD•R;
(2)若△ABC为钝角三角形(∠C为钝角),(1)的结论还成立吗?请画图证明你的结论.
考点:三角形的外接圆与外心,圆周角定理,相似三角形的判定与性质
专题:
分析:(1)连接AO并延长交⊙O于点E,连接CE,根据相似三角形的判定定理得出△ABD∽△AEC,由相似三角形的对应边成比例即可得出结论;
(2)根据题意画出图形,连接AO并延长交⊙O于点E,连接CE,根据相似三角形的判定定理得出△ABD∽△AEC,由相似三角形的对应边成比例即可得出结论.
(2)根据题意画出图形,连接AO并延长交⊙O于点E,连接CE,根据相似三角形的判定定理得出△ABD∽△AEC,由相似三角形的对应边成比例即可得出结论.
解答: (1)证明:如图1所示,
(1)证明:如图1所示,
连接AO并延长交⊙O于点E,连接CE,
∵∠B与∠E是
所对的圆周角,
∴∠B=∠E.
∵AD是△ABC的高,
∴∠ADB=90°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴△ABD∽△AEC,
∴
=
,
∵AE是⊙O的直径,
∴AE=2R,
∴
=
,即AB•AC=2R•AD;
(2)成立.
证明:如图2所示,
连接AO并延长交⊙O于点E,连接CE,
∵∠B与∠E是
所对的圆周角,
∴∠B=∠E.
∵AD是△ABC的高,
∴∠ADB=90°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴△ABD∽△AEC,
∴
=
,
∵AE是⊙O的直径,
∴AE=2R,
∴
=
,即AB•AC=2R•AD.
 (1)证明:如图1所示,
(1)证明:如图1所示,连接AO并延长交⊙O于点E,连接CE,
∵∠B与∠E是
 |
| AC |
∴∠B=∠E.
∵AD是△ABC的高,
∴∠ADB=90°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴△ABD∽△AEC,
∴
| AB |
| AE |
| AD |
| AC |
∵AE是⊙O的直径,
∴AE=2R,
∴
| AB |
| 2R |
| AD |
| AC |
(2)成立.
证明:如图2所示,
连接AO并延长交⊙O于点E,连接CE,
∵∠B与∠E是
 |
| AC |
∴∠B=∠E.
∵AD是△ABC的高,
∴∠ADB=90°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴△ABD∽△AEC,
∴
| AB |
| AE |
| AD |
| AC |
∵AE是⊙O的直径,
∴AE=2R,
∴
| AB |
| 2R |
| AD |
| AC |
点评:本题考查的是三角形的外接圆与外心,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、两条直线被第三条直线所截,同位角相等 |
| B、相等的角是对顶角 |
| C、过一点有且只有一条直线与已知直线平行 |
| D、三角形的外角等于与它不相邻的两个内角的和 |
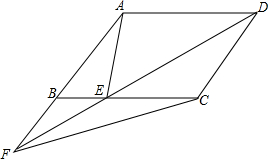 如图,E为平行四边形ABCD的边BC上的一个动点,延长DE交AB的延长线于F,连结AE、AF,
如图,E为平行四边形ABCD的边BC上的一个动点,延长DE交AB的延长线于F,连结AE、AF,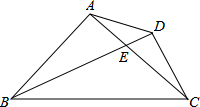 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,若点D为△ABC外一点,且∠ADC=135°,判断BD和CD的位置关系.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,若点D为△ABC外一点,且∠ADC=135°,判断BD和CD的位置关系.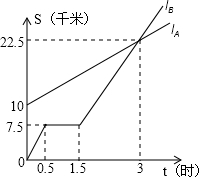 如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
 如图,O是AB的中点,∠A=∠B,△AOC≌△BOD全等吗?
如图,O是AB的中点,∠A=∠B,△AOC≌△BOD全等吗?