题目内容
11.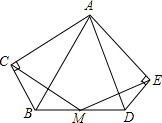 在Rt△ABC和Rt△ADE中,∠BAC=∠DAE,取BD中点M.求证:MC=ME.
在Rt△ABC和Rt△ADE中,∠BAC=∠DAE,取BD中点M.求证:MC=ME.
分析 取AB中点F,AD中点N,连接CF、FM、MN、NE,只要证明△CFM≌△MNE即可.
解答 证明: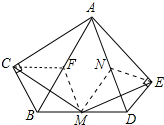 取AB中点F,AD中点N,连接CF、FM、MN、NE.
取AB中点F,AD中点N,连接CF、FM、MN、NE.
∵∠ACB=90°,∠AED=90°,AF=FB,AN=ND,
∴CF=$\frac{1}{2}$AB,NE=$\frac{1}{2}$AD,
∵BM=MD,AF=FB,AN=ND,
∴FM∥AD,MN∥BA,FM=$\frac{1}{2}$AD.MN=$\frac{1}{2}$AB,
∴CF=MN,FM=NE,∠BFM=∠BAD=∠MND,
∵∠CAB+∠CBA=90°,∠DAE+∠ADE=90°,∠CAB=∠DAE,
∴∠CBA=∠ADE,
∵CF=BF,DN=NE,
∴∠FCB=∠CBF,∠NDE=∠NED,
∴∠CFB=∠DNE,
∴∠CFM=∠MNE,
在△CFM和△MNE中,
$\left\{\begin{array}{l}{CF=MN}\\{∠CFM=∠MNE}\\{FM=NE}\end{array}\right.$,
∴△CFM≌△MNE,
∴CM=ME.
点评 本题考查三角形中位线定理、直角三角形斜边中线定理、全等三角形的判定和性质,添加辅助线构造全等三角形是解决问题的关键,属于中考常考题型.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
1.正六边形的内角和为( )
| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
2.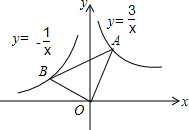 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$,y=$\frac{3}{x}$的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$,y=$\frac{3}{x}$的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$,y=$\frac{3}{x}$的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$,y=$\frac{3}{x}$的图象交于B、A两点,则∠OAB的大小的变化趋势为( )| A. | 逐渐变小 | B. | 保持不变 | C. | 逐渐变大 | D. | 时大时小 |
6.为了解长城小区“全民健身”活动的开展情况,随机对该小区的40名居民一周的体育锻炼时间进行了统计,结果如表:
这40名居民一周体育锻炼时间的中位数是5小时.
| 锻炼时间(时) | 3 | 4 | 5 | 6 | 7 |
| 人数(人) | 6 | 13 | 14 | 5 | 2 |