题目内容
4.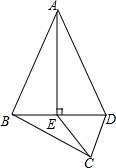 如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )
如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )| A. | 5 | B. | 8 | C. | 10 | D. | 无法计算 |
分析 先在Rt△AEB中根据勾股定理求得BE,再根据等腰三角形的性质得到BD,再根据勾股定理的逆定理得到△BCD是直角三角形,再根据直角三角形的性质可求CE的长度.
解答 解:∵AE⊥BD,AB=13,AE=12,
∴在Rt△AEB中,BE=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∵AB=AD,
∴BD=2BE=10,
∵BC=2$\sqrt{21}$,CD=4,
(2$\sqrt{21}$)2+42=102,
∴△BCD是直角三角形,
∴CE=$\frac{1}{2}$BD=5.
点评 本题考查的是勾股定理,等腰三角形的性质,等腰三角形的性质,直角三角形斜边上的中线,勾股定理的逆定理,根据勾股定理的逆定理得到△BCD是直角三角形是解答此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
14.二次函数y=x2+3x+2的图象与y轴的交点坐标是( )
| A. | (0,2) | B. | (0,3) | C. | (2,0) | D. | (3,0) |
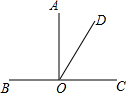 如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.
如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.
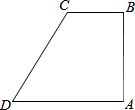 如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为2或2$\sqrt{3}$或4.
如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为2或2$\sqrt{3}$或4.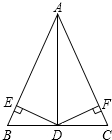 如图,在△ABC中,AD是△ABC中的角平分线,BD=CD,DE⊥AB,DF⊥AC,请你在图中找出三对全等的三角形,并任选一对进行证明.
如图,在△ABC中,AD是△ABC中的角平分线,BD=CD,DE⊥AB,DF⊥AC,请你在图中找出三对全等的三角形,并任选一对进行证明.